PERMÜTASYON

n tane birbirinden farklı elemanın alınıp düzenlenmesine permütasyon denir.

Teorem : n tane farklı elemanın hepsi sıralandığından oluşan düzenlerin sayısı n! kadardır.

İspat : Doldurulacak n tane yer vardır. 1. yere n tane, 2. yere (n–1) tane, ....., n’inci yere 1 tane eleman yerleştirme ihtimali vardır. n.(n–1).......2.1 = n! olur. Bu durum P(n, n) ile gösterilir.

Teorem (Tekrarlı Permütasyon) : n tane nesnenin n₁ tanesi bir türden, n₂ tanesi ikinci türden, n₃ tanesi üçüncü türden, ......, n_k tanesi k’ıncı türden ise bu nesnenin tümü sıralandığında elde edilecek farklı düzen sayısı :

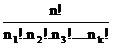 olur.n=n₁ + n₂ + . . . + n_k

ÖRNEK : 7 tane topu, 7 tane kutuya, kutulardan ikisinde 2, üçünde 1 ve ikisi de boş olmak şartıyla kaç farklı şekilde yerleştirilir?

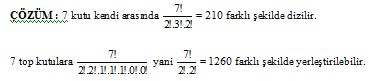
ÖRNEK : 52 kartlık standart bir deste 4 oyuncu arasında kaç farklı şekilde dağıtılır?

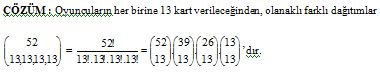
ÖRNEK : 3, 2, 2, 3, 7 rakamları ile yazılabilecek 5 basamaklı sayıların ne kadarı 2 ile başlar 7 ile biter?

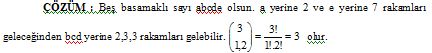
Tanım : n elemanlı bir A kümesinin r elemanının alınıp sıralanmasıyla elde edilen permütasyona, n’nin r’li permütasyonu denir ve böyle permütasyonların toplam sayısı P(n, r) ile gösterilir.

NOT : Bu r nesne tekrarlı olarak n^r farklı şekilde sıralanabilir.

ÖRNEK : 5 kişi bir taksiye ikisi önce, üçü arkada oturmak koşuluyla kaç farklı biçimde binebilirler? (Oturuşlarda yerlerin değişmesi farklı diziliş sayılacaktır.)

ÇÖZÜM : (P5,3).P(2,2) = 5.4.3.2.1. = 120 değişik şekilde taksiye binebilirler.

ÖRNEK : Bir adamın 8 çift eldiveni vardır. Bu kimse birbirine uymayan bir sol ve bir sağ eldiveni kaç yolla seçebilir?

ÇÖZÜM : İlk eldiven 8 farklı şekilde, ikincisi 7 farklı seçilebilir. O halde 8.7 = 56 uygun seçim yapılır.

ÖRNEK : 52’lik bir briç destesinden alınan 5 kartın permütasyonlarının sayısını yazınız.

ÖRNEK : 1, 2, 3, 4, 5 rakamlarıyla ne kadar 4 basamaklı sayı yazılabilir?

a)      Rakamlar yinelenmiyor (Kullanılan bir daha kullanılmıyor)

b)      Yinelemeye izin veriliyor.

c)      Rakamların her birini yinelemeden tek sayı olması isteniyor.

ÇÖZÜM :

a) Doldurulabilecek 4 yer vardır. İlk yer 5 rakamdan herhangi biri ile 5 farklı yolla doldurulur. İkinci yer geri kalan 4 rakamdan herhangi biri ile 4 yolla doldurulur. Benzer şekilde, üçüncü yer 3 yolla, dördüncü yer 2 yolla doldurulabilir. Çarpma kuralından, istenen yanıt;

5.4.3.2 = 120 bulunur.

b) Rakamların yinelenmesine izin verildiğinde 4 yerin her biri 5 rakamın herhangi biri ile, yani 5 yolla doldurulur. O halde 4 basamaklı sayıların sayısı 5.5.5.5 = 625’tir.

c) Dört basamaklı sayı tek olacağından son rakam 1 veya 3 yada 5 olmak zorundadır. Bu nedenle dördüncü yer 3 yolla doldurulur. Bu işlem yapıldıktan sonra geri kalan yerler sırasıyla 4, 3, ve 2 yolla doldurulabilir. O halde istenen yanıt;

4.3.2.3 = 72’dir.

NOT : Bu örneğin (c) şıkkında dördüncü yeri önce doldurduk. Buradaki gibi bir işlem özel bir yolla yapılmak zorunda ise genellikle onu önce yapmayı önerebiliriz. Geri kalanlardan hangisinin önce yapılacağı önemli değildir.

Teorem : Bir çember üzerinde düzenlenecek n farklı nesnenin permütasyonlarının sayısı (n–1)!’dir.

ÖRNEK : 4 evli çift yuvarlak masa etrafında eşler daima yan yana oturmak koşulu ile kaç farklı şekilde oturabilirler?

ÇÖZÜM :

(4–1)! = 3! = 6

2! = 2

4 çift var : 2.2.2.2 = 16

16.6 = 96 farklı şekilde oturabilirler.