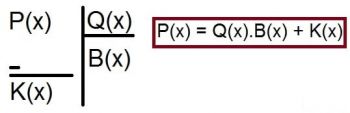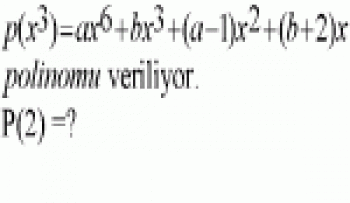Polinomlar Konu Anlatımı

Polinomlar konusu matematik için önemli bir konudur. Bu ders notunda polinomlar üzerinde duracağız ve nedir ne değildir öğrenmeye çalışacağız.

n doğal sayı a0, a1, a2, .... , an gerçel sayılar ve x değişken olmak üzere,

P(x) = a0 + a1x + a2x2 + .... + anxn şeklinde tanımlanan ifadelere gerçel katsayılı bir bilinmeyenli polinom denir.

• P(x) polinomunda a0, a1, a2, .... , an gerçel sayılarına polinom katsayıları denir.
• P(x) polinomunda a0 + a1x + a2x2 + .... + anxn ifadelerine polinom terimleri denir.
• P(x) polinomunda derecesi en büyük olan terimin katsayısına polinom baş katsayısı denir.
• P(x) polinomunda x in en büyük kuvveti olan doğal sayıya P(x) polinomunun derecesi denir ve der (P(x)) ile gösterilir.
• Tüm katsayıları sıfır olan polinoma sıfır polinomu denir.

Sıfır polinomunun derecesi belirsizdir.

• P(x) = a0 + a1x + a2x2 + .... + anxn polinomunda a0 ≠ 0, a1 = a2 = ..... = an = 0 ise P(x) polinomuna sabit polinom denir ve P(x) = a0 şeklinde gösterilir.

Sabit polinomun derecesi 0 dır.

İki Değişkenli Polinomlar

Katsayıları reel sayı, x ve y değişkenlerinin kuvvetlerinin kuvvetleri doğal sayı olmak üzere, P(x, y) şeklindeki polinomlara iki değişkenli polinom denir.

 

 

Örnek: P(x, y) = 2xy2 - 3x2y3 + 4

olduğuna göre P(1, -1) kaçtır?

Çözüm:

P(x, y) = 2xy2 - 3x2y3 + 4

P(1, -1) = 2.1.(-1)2 - 3.12.(-1)3 + 4

= 2 + 3 + 4

= 9

Örnek: P(x, y) = x4y3 - 2x5 + y6 -3x5y4

olduğuna göre P(x, y) polinomunun derecesi kaçtır?

Çözüm: P(x, y) polinomunun derecesi a.xn.yn terimindeki n + m toplamının en büyük olanıdır.

 

3x5.y4 teriminde 5 + 4 = 9 toplamı en büyük olduğundan polinomun derecesi 9 dur.

İki Polinomun Eşitliği

İki polinomun eşit olabilmesi için dereceleri aynı olan terimlerin katsayıları da aynı olmalıdır.

P(x) = a0 + a1x + a2x2 + ..... + anxn

Q(x) = b0 + b1x + b2x2 + ..... + bnxn

polinomlarında P(x) = Q(x) olabilmesi için

a0 = b0, a1 = b1, a2 = b2, an = bn

olmalıdır.

Örnek:

(a - 1)x3 + 4x2 + c + 2 = 3x3 + (b - 1)x2 + (2 - d)x

olduğuna göre a + b + c + d toplamı kaçtır?

Çözüm:

Aynı dereceli terimlerin katsayıları eşit olmalıdır.

Yani;

a -1 = 3, b - 1 = 4, 2 - d = 0, c + 2 = 0

a = 4, b = 5, d = 2, c = -2

O halde, a + b + c + d = 4 + 5 - 2 + 2 = 9

Örnek:

P(x) = (2x - 3)(x + a)

Q(x) = 2x2 - x + b

P(x) = Q(x) olduğuna göre, a.b çarpımı kaçtır?

Çözüm:

P(x) = Q(x)

(2x - 3)(x + a) = 2x2 - x + b

2x2 + x(2a - 3) - 3a = 2x2 - x +b

Aynı dereceli terimlerin katsayıları eşit olmalıdır.

2a - 3 = -1 , b = -3a

a = 1 b = -3

O halde; a.b = 1.(-3) = -3 tür.

Örnek:

P(x) = x2 + nx - 5

Q(x) = 9x + m

P(3x - 1) = Q(x2 - x)

olduğuna göre m - 2n farkı kaçtır ?

Çözüm:

P(3x - 1) = Q(x2 - x) eşitliğinde x yerine 1 yazalım

P(2) = Q(0)

22 + 2n - 5 = 9.0 +m

m - 2n = -1

Polinomlarda Toplama ve Çıkarma İşlemi

İki polinom arasında toplama veya çıkarma işlemi yapılırken, aynı dereceden terimlerin katsayıları toplanır veya çıkarılır.

a.xn + b.xn = (a + b).xn

a.xn - b.xn = (a - b).xn

Örnek:

P(x) = x3 - 3x2 + 5x + 1

Q(x) = x2 + 4x + 4

olduğuna göre P(x) - Q(x) fark polinomu aşağıdakilerden hangisidir ?

A) x3 + 4x2 - 5x + 1 B) x3 + x2 - x -3 C) x3 + 4x2 - x +5

D) x3 - 4x2 + x -5 E) x3 - 4x2 + x -1

Çözüm:

P(x) - Q(x) = (x3 - 3x2 + 5x - 1) - (x2 + 4x + 4)

= x3 - 3x2 + 5x - 1 - x2 - 4x - 4

= x3 - 4x2 + x + 5 (Cevap : D)

Örnek:

P(x) + P(x + 2) = 4x + 2

olduğuna göre P(-2) kaçtır ?

Çözüm:

I. dereceden iki polinomun toplamı birinci dereceden bir polinom olduğuna göre P(x) = ax + b olmalıdır.

P(x) + P(x + 2) = 4x + 2

ax + b + a(x + 2) + b = 4x + 2

ax + b + ax + 2a + b = 4x + 2

2ax + 2a + 2b = 4x + 2

İki polinomun eşitliğinden ,

2a = 4 ve 2a + 2b = 2

a =2 4 + 2b = 2

b = -1

Buna göre; P(x) = ax + b = 2x - 1 dir.

x = -2 için P(-2) = 2.(-2) - 1

= -5 tir.

Polinomlarda Çarpma işlemi

P(x) ve Q(x) polinomları çarpılırken I. polinomun her bir terimi II. polinomun her bir terimi ayrı ayrı çarpılarak toplanır.

Örnek:

P(x) = x3 - 4x + 1

Q(x) = x2 + x

H(x) = P(x).Q(x)

olduğuna göre H(1) değeri kaça eşittir ?

Çözüm:

I. Yol:

H(1) = P(1). Q(1) olduğuna göre

P(1) = 13 - 4.1 + 1 = -2

Q(1) = 12 + 1 = 2

H(1) = P(1). Q(1) = 2.(-2) = -4 tür.

II. Yol:

H(x)= P(x). Q(x)

H(x) = (x3 - 4x +1). (x2 + x)

H(x) = x5 + x4 - 4x3 - 4x2 + x2 + x

H(x) = x5 + x4 - 4x3 - 3x2 + x

H(1) = 15 + 14 - 4.13 - 3.12 + 1

H(1) = 1 + 1 - 4 - 3 + 1 = -4 tür.

Uyarı: Çarpım polinomunun derecesi, çarpanların dereceleri toplamına eşittir. der(P(X).Q(x)) = der(P(x)) + der(Q(x))

Örnek:

P(x) = 2x3 - 3x + 1

Q(x) = x4 - 5x2 + 3

olduğuna göre, [P(x2)].[Q(x3)]2 çarpım polinomunun derecesi kaçtır ?

Çözüm:

Bir polinomun derecesi bulunurken en büyük dereceli terimler alınarak işlem yapılır.

P(x) polinomunun derecesi 3 olduğundan P(x) = x3

Q(x) polinomunun derecesi 4 olduğundan Q(x) = x4

alınabilir.

O halde; P(x2).[Q(x3)]2 = (x2)3.[(x4)3]2

= x6.x24

= x30

olduğuna göre bu polinomun derecesi 30 dur.

Örnek:

ax3 + bx2 + cx + d = (x - 3).(x2 + 2x - 1)

olduğuna göre, b - c - a + d ifadesinin değeri kaçtır ?

Çözüm:

ax3 + bx2 + cx + d = (x - 3).(x2 + 2x + 1)

eşitliğinde x = -1 yazalım.

-a + b - c + d = (-1 -3).(1 -2 -1)

b - c - a + d = (-4).(-2)

= 8 dir.

Uyarı: P(x) = a0 + a1x + a2x2 + a3x3 + a4x4 polinomunda

• x = 1 yazılarak katsayılar toplamı bulunur. P(1) = a0 + a1 + a2 + a3 + a4
• x = 0 yazılarak sabit terim bulunur. P(0) = a0
• P(x) in çift dereceli terimlerinin katsayıları toplamı: [P(1) + P(-1)] / 2
• P(x) in tek dereceli terimlerinin katsayıları toplamı: [P(1) - P(-1)] / 2

• Örnek:

  P(x) = 2x3 - x2 + 2x -5

  olduğuna göre, P(x - 2) polinomunun katsayılar toplamı kaçtır ?

  Çözüm:

  P(x - 2) polinomunun katsayılar toplamı sorulduğundan x = 1 değerini bu polinomda yerine yazalım.

  x = 1 için P(1 - 2) = P(-1) in değerini bulmalıyız.

  P(x) = 2x3 - x2 + 2x - 5 ifadesinde P(-1) i bulmak için x = -1 yazalım.

  x = -1 için P(-1) = 2.(-1)3 - (-1)2 + 2(-1) - 5

  = -10

Polinomlarda Bölme İşlemi

Polinomlarda bölme işlemi ile ilgili birçok soru gelmektedir. Özellikle kalan bulma soruları polinomlar konusundan en çok soru gelen yerdir.

der(P(x)) ≥ der(Q(x)) ve Q(x) ≠ 0 olmak üzere, P(x) polinomunun Q(x) ile bölümünde bölüm B(x), kalan K(x) olsun.

• P(x) = Q(x).B(x) + K(x)
• der(K(x)) < der(Q(x))
• K(x) = 0 ise P(x) polinomu Q(x) polinomuna tam bölünür.

• Örnek:

  P(x) = 3x3 - 2x2 + 5

  polinomunun (x - 1) ile bölümünden kalan kaçtır ?

  Çözüm:

  P(x) polinomunun (x - 1) ile bölümünden bölüm B(x), kalan K ise

  3x3 - 2x2 + 5 = (x - 1).B(x) + K

  x = 1 için 3.13 - 2.12 + 5 = (1 - 1).B(1) + K

  3 - 2 + 5 = K

  K = 6 dır.

  Örnek:

  P(x) = x2 + x + n

  polinomunun (x + 3) ile bölümünden kalan 5 olduğuna göre, n kaçtır ?

  Çözüm:

  P(x) polinomunun (x + 3) ile bölümünden kalan 5 ise P(-3) = 5 tir.

  x = -3 için P(-3) = (-3)2 + (-3) + n

  5 = 6 + n

  n = -1

• P(x) polinomunun (x - m) ile bölümünden kalan K ise, P(m) = K dır.
• P(m) = 0 ise (x - m) ifadesi P(x) polinomunun bir çarpanıdır.
• Polinomlarda kalan sorulduğunda, bölen sıfıra eşitlenerek bulunan x değeri, bölünen polinomda x yerine yazılır.

• Örnekler:

  • P(x) polinomunun (6x - 3) ile bölümünden kalan 2 ise, P(½ ) = 2 dir.
  • P(x + 3) polinomunun (x - 4) ile bölümünden kalan 4 ise, P(7) = 4 tür.
  • P(4x - 2) polinomunun sabit terimi -5 ise, P(-2) = -5 tir. (Sabit terim için x yerine 0 yazılır).
  • P(5x - 3) polinomunun katsayılar toplamı 6 ise, P(2) = 6 dır. (Katsayılar toplamı için x yerine 1 yazılır.)
  • (x - 3).P(x) + x3.Q(x) polinomunun x - 1 ile bölümünden kalan 8 ise, (1 - 3).P(1) + 1.Q(1) = 8 ve -2.P(1) + Q(1) = 8 dir.

  Örnek:

  P(x - 2) polinomunun (x + 1) ile bölümünden kalan 3, Q(x + 2) polinomunun (x - 1) ile bölümünden kalan 5 tir.

  Buna göre, P(x - 6) + Q(x) polinomunun (x - 3) ile bölümünden kalan kaçtır ?

  Çözüm:

  P(x - 2) polinomunun (x + 1) ile bölümünden kalan 3 ise, P(-3) = 3 tür.

  Q(x + 2) polinomunun (x - 1) ile bölümünden kalan,

  P(3 - 6) + Q(3) = P(-3) + Q(3)

  = 3 + 5= 8 dir.

  Dikkat: Bölen çarpanlarına ayrılmıyor veya çarpanları köklü ifadelerden oluşuyorsa kalanını bulmak için, bölen polinom sıfıra eşitlenir ve x in en büyük dereceli terimi yalnız bırakıldıktan sonra bölünen polinomda yerine yazılır.

  Örnek:

  P(x) = x3 - x2 - 2x - 1

  polinomunun (x2 - x + 2) ile bölümünden kalan aşağıdakilerden hangisidir ?

  A) 2x - 1 B) -4x - 1 C) 4x + 1 D) x + 4 E) x - 4

  Çözüm:

  P(x) polinomunun (x2 - x + 2) ile bölümünden kalan bulmak için ( x2 - x + 2 = 0 ise x2 = x - 2 olduğundan ) P(x) polinomunda x2 yerine (x - 2) yazalım.

  P(x) = x2.x - x2 - 2x - 1