SaymanınTemel Kuralları
1) TOPLAMA YOLU İLE SAYMA
Soru) Farklı özellikte, 3 matematik ve 5 kimya kitabı arasından 1 matematik veya 1 kimya kitabı kaç yolla seçilebilir?
“veya” toplama yapacağımız anlamına gelir
2) ÇARPMA YOLU İLE SAYMA
İlk işlem m yolla yapılabiliyorsa ve ilk işlem bu m yoldan birisiyle yapıldıktan sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m.n yolla yapılabilir.
Soru)Farklı özellikte 2 matematik ve 3 fizik kitabı arasından 1 matematik ve 1 fizik kitabı kaç yolla seçilebilir?

Şimdi her şeyden önce
Eğer SEÇİLİM yapacaksak KOMBİNASYON …..C(n,r)
Eğer SIRALAMA yapacaksak FAKTÖRİYEL …..n!
Eğer SEÇME+SIRALAMA yapacaksak PERMÜTASYON….P(n,r)
PERMÜTASYON
n tane birbirinden farklı elemanın alınıp düzenlenmesine permütasyon denir.
Bunların kendi içinde değişimleri her seferinde farklı bir durum ortaya çıkarır.Tüm durumları eğer koşul yoksa n! İle ifade ederiz.
Permütasyon seçme+sıralama olduğundan
Seçme işlemi C(n,r)
Sıralama işlemi n!
İkisi birlikte C(n,r)*n!= P(n,r)
O zaman P(n,r)=(n!)/(n-r)! dir
Permütasyonlarda birbirinden farklı elemanların değişik
sıralanışları söz konusudur.
Permütasyonolan ifadeler genelde;
• Kaç türlü sıralanabilir? Dizilebilir? Poz verebilir?
• Kaç türlü sayı yazılabilir? Anlamlı yada anlamsız kaç türlü
kelimeyazılabilir?
• Yuvarlak masa etrafında kaç türlü oturulabilir? Şeklindedir
2. Dairesel dönel permütasyon
n elemanlı bir kümenin elemanlarının, bir çemberin etrafında
birbirinden farklı dizilişlerinden her birine, dairesel permütasyon denir.
n elemanlı bir çember etrafında;
(n-1)! Farklı bir şekilde sıralanır
Örnek:
7 kişilik bir aile, anne ile baba yan yana oturmak şartıyla, daire
şeklindekibir masa etrafına kaç değişik şekilde oturabilirler?
A) 24 B) 48 C) 120 D) 240 E) 90


Örnek:
MATEMATİK kelimesindeki harflerle anlamlı yada anlamsız kaç kelimeyazılabilir?
A) 9! B) 8! C) 45360 D) 32424 E) 7!
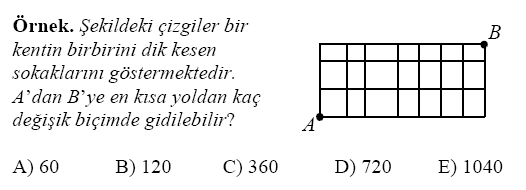
SORU:

Çözüm:


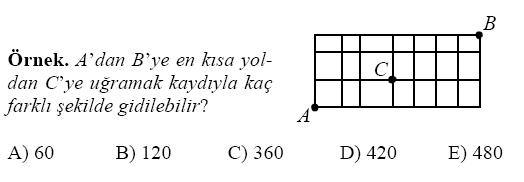
KOMBİNASYON
n elemanlı bir kümenin r elamanlı alt kümelerinin sayısına C(n,r) denir.Biz buna kombinasyon diyoruz.yani belirli bir sayıda elemanı olan kümeden alabileceğimiz alt kümeler var. Bunların hepsinin toplamı 2^n(2 üzeri n idi). Bize 3 elemanlı alt kümeleri dendiğinde C(n,3) alacağız.
Peki C(n,r) nasıl bulunuyor.
C(n,r)= (n!)/(n-r)!*r! dir



SON ….





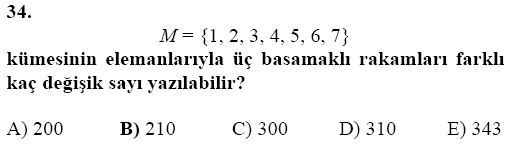


Yorumlar15
çözüm yok
ayıp ayıp ulen cevap anahtarı nerde !!
vgfdfgdgdgd
Hocam zaten web üzerinde aman aman bir konu anlatımı beklemek olanaksız. Ama bence sorular güzel. Belki sorularımızdan yararlanabilirsiniz.
Eleştiriniz için teşekkürler...
Hayatımda böyle saçma konu anlatımı görmedim.
Yorumlarınızı Bekliyoruz
Yorum Yazın
Yorum Yapın