Permütasyon Konusu
Saymanın Temel Kuralları
1)TOPLAMA YOLU İLE SAYMA
Soru) Farklı özellikte, 3 matematik ve 5 kimya kitabı arasından 1 matematik veya 1 kimya kitabı kaç yolla seçilebilir?
“veya” toplama yapacağımız anlamına gelir
Çözüm:
3+5=8 elemanlıdır.Yani seçme 8 yolla yapılabilir.Diğer bir ifadeyle, 3 matematik ve 5 kimya kitabı arasından 1 matematik veya 1 kimya kitabı 3+5=8 yolla seçilebilir.
2)ÇARPMA YOLU İLE SAYMA
İlk işlem m yolla yapılabiliyorsa ve ilk işlem bu m yoldan birisiyle yapıldıktan sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m.n yolla yapılabilir.
Soru)Farklı özellikte 2 matematik ve 3 fizik kitabı arasından 1 matematik ve 1 fizik kitabı kaç yolla seçilebilir?
Çözüm:
2 matematik ve 3 fizik kitabı arasından 1 matematik ve 1 fizik kitabı 2.3=6 yolla seçilebilir.
Soru) A kenti ile B kenti arasında 2 değişik yol,B ile C kenti arasında ise 5 değişik yol vardır.A kentinden C kentine gitmek isteyen bir kimse B den geçmek koşulu ile;
a) Kaç değişik yol ile A şehrinden C şehrine gidebilir?
b) A şehrinden C şehrine kaç değişik yol ile gidip dönebilir?
c) Kullandığı yolu bir kez daha kullanmamak koşulu ile C şehrine kaç değişik yoldan gidip gelebilir?
Çözüm :
a) Bir kimse A şehrinden B şehrine gitmek için 2 farklı yoldan birini B den C ye gitmek için de 5 farklı yoldan birini kullanmak zorundadır.Saymanın temel ilkesine göre A dan C ye, B ye uğrayarak 2.5= 10 değişik biçimde gidebilir.
b) A şehrinden B şehrine gitmek için 2 farklı yoldan birini, B şehrinden C şehrine gitmek içinde 5 farklı yoldan birini seçebilir.C şehrinden B şehrine geri dönerken 5 farklı yoldan biri, b den a ya dönerken de 2 farklı yoldan birini seçebileceğinden A dan C ye 2.5.5.2 = 100 değişik biçimde gidip ve gelebilir.
c) Adan C ye 2.5 = 10 farklı şekilde gidebilir C şehrinden B şehrine geri dönerken gidişte yollardan biri kullanıldığından geriye kalan 5- 1 =4 farklı yolun biri ve B den A ya dönerken de gidişte yollardan biri kullanıldığından geri kalan (2-1) =1 farklı yoldan biri kullanılır.Öyleyse C den A ya dönüş 4.1 = 4 değişik biçimde olur.Saymanın temel ilkesine göre A dan C ye gidiş ve dönüş 2.5.4.1=40 değişik biçimde olur.
Şimdi her şeyden önce Eğer SEÇİLİM yapacaksak
KOMBİNASYON …..C(n,r) Eğer SIRALAMA yapacaksak
FAKTÖRİYEL …..n! Eğer SEÇME+SIRALAMA yapacaksak
PERMÜTASYON….P(n,r)
PERMÜTASYON
n tane birbirinden farklı elemanın alınıp düzenlenmesine permütasyon denir. Bunların kendi içinde değişimleri her seferinde farklı bir durum ortaya çıkarır.Tüm durumları eğer koşul yoksa n! İle ifade ederiz. Permütasyon seçme+sıralama olduğundan seçme işlemi C(n,r)
Sıralama işlemi n!
İkisi birlikte C(n,r)*n!= P(n,r)
O zaman P(n,r)= (n!)/(n-r)! dir
Permütasyonlarda birbirinden farklı elemanların değişik sıralanışları söz konusudur.
Permütasyon olan ifadeler genelde;
Kaç türlü sıralanabilir? Dizilebilir? Poz verebilir?
Kaç türlü sayı yazılabilir?
Anlamlı yada anlamsız kaç türlü kelime yazılabilir?
Yuvarlak masa etrafında kaç türlü oturulabilir?
Şeklindedir Soru
Örnek:
A={1,2,3,4,5,6} kümesinin elemanları ile iki basamaklı ve basamaklarındaki rakamlar birbirinden farklı kaç sayı yazılabilir
A)12 B) 24 C) 60 D) 120 E) 240 Örnek:
Bir rafta 5 tane matemaik, 2 tane edebiyat ve 3 tane tarih kitabı vardır. Aynı tür kitaplar birbirinden ayrılmamak üzere, kaç değişik şekilde yan yana sıralanabilir?
A)30 B) 90 C) 1440 D)8640 E)8460
2. Dairesel dönel permütasyon
n elemanlı bir kümenin elemanlarının, bir çemberin etrafında birbirinden farklı dizilişlerinden her birine, dairesel permütasyon denir.
n elemanlı bir çember etrafında; (n-1)! Farklı bir şekilde sıralanır
Örnek:
7 kişilik bir aile, anne ile baba yan yana oturmak şartıyla, daire şeklindeki bir masa etrafına kaç değişik şekilde oturabilirler?
A) 24 B) 48 C) 120 D) 240 E) 90
Örnek:
MATEMATİK kelimesindeki harflerle anlamlı yada anlamsız kaç kelime yazılabilir?
A) 9! B) 8! C) 45360 D) 32424 E) 7!
SAYMANIN TEMEL KURALI
1. Toplama Kuralı
Sonlu ve ayrık kümelerin eleman sayılarının toplamı, bu kümelerin birleşimlerinin elemanlarının sayısına eşittir.
Sonlu ve ayrık iki küme A ve B olsun.
s(A)=m, s(B)=n, s(A ∩ B)= Ø olmak üzere,
s(A ∪ B)=s(A)+s(B)= m + n dir.
Sonuç
Ayrık iki işlemden biri m yolla diğeri n yolla yapılabiliyorsa, bu işlemlerden biri veya diğeri m + n yolla yapılabilir.
2. Çarpma Kuralı
2 tane elemandan oluşan ( a1 , a2) ifadesine sıralı ikili denir. Benzer biçimde
( a1 , a2 , a3 ) ifadesine sıralı üçlü
( a1 , a2 , a3 , a4) ifadesine sıralı üçlü
. . .
(a1 , a2 , a3 , ...,an) ifadesine sıralı n li denir.
A ve B sonlu iki küme olsun
s(A) = m
s(B) = n olmak üzere,
s(A × B) = s(A) × s(B) = m × n dir.
A × B kümesi birinci bileşenleri A dan ikinci bileşenleri B den alınan sıralı ikililerden oluşur.
Sonuç
İki işlemden birincisi m yolla yapılabiliyorsa ve ilk işlem bu m yoldan birisiyle yapıldıktan sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m × nyolla yapılabilir.
FAKTÖRİYEL
1 den n ye kadar olan sayma sayılarının çarpımına n faktöriyel denir ve n! biçiminde gösterilir.
0!=1
1!=1
2!=1.2=2
3!=1.2.3=6
4!=1.2.3.4=24
Sonuç
n!=n.(n-1)!=n.(n-1).(n-2)!
PERMÜTASYON (SIRALAMA)
r ve n sayma sayısı ve r ≤ n olmak üzere, n elemanlı bir kümenin r elemanlı sıralı r lilerine bu kümenin r li permütasyonları denir.
n elemanlı kümenin r li permütasyonlarının sayısı :
P(n,r)=
P(n, n) = n!
P(n, 1) = n
Dairesel (Dönel) Permütasyon
n tane farklı elemanın dönel (dairesel) sıralamasına, n elemanın dönel (dairesel) sıralamasıdenir.
Elemanlardan biri sabit tutularak n elemanın dönel (dairesel) sıralamalarının sayısı (n – 1)! ile bulunur.
Tekrarlı Permütasyon
n tane nesnenin n1 tanesi 1. çeşitten, n2 tanesi 2. çeşitten, … , n2 tanesi de r. çeşitten olsun.
n =n1, n2, n3,…, nr olmak üzere bu n tane nesnenin n li permütasyonlarının sayısı,Permütasyon ile İlgili Yazılar
Permütasyon Üst Düzey Anlatım
PERMÜTASYON
n tane birbirinden farklı elemanın alınıp düzenlenmesine permütasyon denir.
Teorem : n tane farklı elemanın hepsi sıralandığından oluşan düzenlerin sayısı n! kadardır.
İspat : Doldurulacak n tane yer vardır. 1. yere n tane, 2. yere (n–1) tane, ....., n’inci yere 1 tane eleman yerleştirme ihtimali vardır. n.(n–1).......2.1 = n! olur. Bu durum P(n, n) ile gösterilir.
Teorem (Tekrarlı Permütasyon) : n tane nesnenin n1 tanesi bir türden, n2 tanesi ikinci türden, n3 tanesi üçüncü türden, ......, nk tanesi k’ıncı türden ise bu nesnenin tümü sıralandığında elde edilecek farklı düzen sayısı :
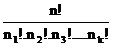 olur.
olur.
Permütasyon Kombinasyon
SaymaninTemel Kurallari
1) TOPLAMA YOLU İLE SAYMA
Soru) Farklı özellikte, 3 matematik ve 5 kimya kitabı arasından 1 matematik veya 1 kimya kitabı kaç yolla seçilebilir?
“veya” toplama yapacağımız anlamına gelir
Çözüm:
2) ÇARPMA YOLU İLE SAYMA
ilkişlem m yolla yapılabiliyorsa ve ilk işlem bu m yoldan birisiyle yapıldıktan sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m.n yolla yapılabilir.
Soru)Farklı özellikte 2 matematik ve 3 fizik kitabı arasından 1 matematik ve 1 fizik kitabı kaç yolla seçilebilir?

