Türev işleminin tersi integraldir. f(x)'in türevi g(x) ise g(x)'in integrali f(x)'tir. (Bir sabit sayı farkla) Bu makalede tüm integral türleri için çözüm yollarını inceleyeceğiz. Bazı ifadelerin integralinin alınması, türev bilgisine dayalı aşağıdaki formüllerin bilinmesi suretiyle oldukça kolaydır. Bu makalede bu tür integral hesaplamaları yapılacaktır.  

MAKELENİN İÇERİĞİ:

BELİRSİZ İNTEGRAL

BELİRSİZ İNTEGRAL ÖZELLİKLERİ VE FORMÜLLERİ

DEĞİŞKEN DEĞİŞTİRME YÖNTEMİ

TRİGONOMETRİK İFADELERİN İNTEGRALİ

KISMİ İNTEGRAL

Belirsiz İntegral

Türevi f(x)  veya diferansiyeli f(x)dx olan F(x) fonksiyonuna f(x) fonksiyonunun belirsiz integrali denir. 

Belirsiz İntegral Özellikleri ve Formülleri

SORULAR

1-3: 

4-6:

7-9:

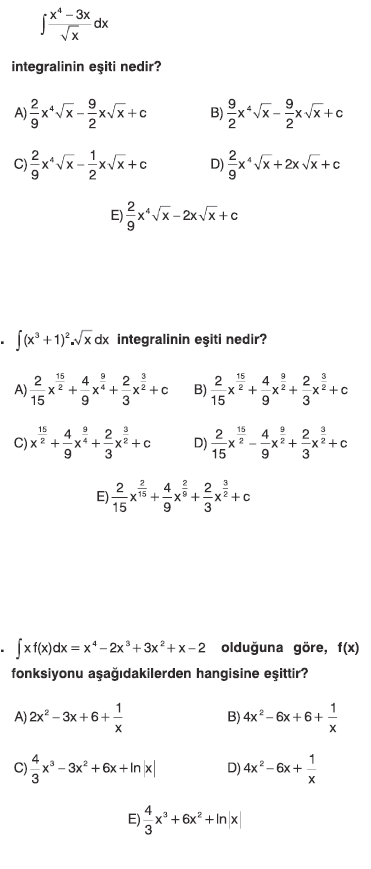
10-12:

Cevaplar

1-3:

4-6:

7-8:

9-

10-11:

12-

Değişken Değiştirme Yöntemi

Bazı ifadeler için integral alma işlemi, yani integrali alınacak olan ifadenin hangi ifadenin türevi olduğunu görmek zordur. Çeşitli integral alma yöntemleriyle bu zorluğun üstesinden gelinmiştir.

Bu yöntemler sırasıyla şöyledir:

1. Değişken Değiştirme

2. Basit kesirlere ayırma

3. Trigonometrik ifadelerin integrali 

4. Kısmi integral

1. Değişken Değiştirme Yöntemi

 ∫ f(x) dx integralinde x=g(u) biçiminde uygun değişken değişimi yapılır. Değişimden sonra diferansiyel alınır. f(x) fonksiyonu ve dx diferansiyeli u'ya bağlı olarak yeniden yazılır. İntegral hesaplanır. u yerine x cinsinden ifadesi yazılarak sonuca ulaşılır.

Genel olarak,

a) Polinom ise derecesi büyük olana,

b) Kesirli ise paydasına,

c) Köklü ise kök içine,

d) Üslü ise üssüne u denilir.