ÖRNEK

19. terimi 42 ve 33. terimi 88 olan aritmetik dizinin 26. terimi kaçtır?

a₁₉ = 42 ve a₃₃ = 88 ve (19 + 33)/2 = 26 olduğu için,

a₂₆ = (a₁₉+a₃₃)/2

a₂₆ = (42+88)/2

a₂₆ = 65’tir.

GEOMETRİK DİZİ

A.     TANIM

Ardışık iki terimin oranı aynı sabit bir sayı olan dizilere geometrik dizi denir. Diğer bir ifadeyle

n ∈ N⁺ için, a_{n + 1}/a_n= r olacak şekilde bir r ∈R varsa (a_n) dizisine geometrik dizi, r sayısına ortak a_n çarpan veya ortak oran denir.

ÖRNEK

(a_n) = (2ⁿ⁺⁵) dizisinin geometrik dizi olduğunu gösteriniz. Dizinin ortak çarpanını bulunuz.

(a_n+1)/a_n = (2ⁿ⁺¹⁺⁵)/2ⁿ⁺⁵ = 2olduğuna göre (a_n), ortak çarpanı r = 2 olan geometrik bir dizidir.

B.GENEL TERİM

Dizinin ilk terimi a₁ ve ortak çarpanı r olsun. Bu durumda,

a₁ = a₁

a₂ = r.a₁

a₃ = r.a₂ = r².a₁

a₄ = r.a₃ = r³.a₁

Demek ki, geometrik dizinin genel terimi: a_n = r^{n – 1}.a₁ veya a_n = r^{n – p}.a_p dir.

ÖRNEK

İlk terimi 14 ve ortak çarpanı ½ olan geometrik dizinin genel terimi nedir?

a₁ = 4 ve r = ½

a_n = r^{n – 1} . a₁

a_n = (1/2)^{n – 1} . 4

a_n = 2^{3 - n}

A.GEOMETRİK DİZİNİN ÖZELLİKLERİ

Geometrik dizide a_p ve a_k biliniyorsa, ortak çarpan : r^{p – k} = a_p/a_k  eşitliğinde bulunur.

ÖRNEK

2. terimi 3/5 ve 5. terimi 75 olan geometrik dizinin ortak çarpanı nedir?

a₂ = 3/5 ve a₅ = 75

r^{5 – 2} = a₅/a₂

r³ = 75/3/5

r³ = 125

r = 5 tir.

Geometrik dizinin ilk n teriminin toplamı S_n ile gösterilirse S_n = a₁.(1 – rⁿ)/(1-r) olur.

SONUÇ:

Sabit dizi, ortak farkı 0 olan aritmetik bir dizidir. Sabit dizi, ortak çarpanı 1 olan geometrik bir dizidir. Sabit dizi, ortak çarpanı 1 olan geometrik bir dizidir. Yani, sabit dizi hem aritmetik hem de geometrik dizidir.

ÖRNEK:

Bir geometrik dizinin ilk terimi x, ortak çarpanı 6, n. terimi y’dir. Bu dizinin, ilk n teriminin toplamının x ve y’ye bağlı ifadesi aşağıdakilerden hangisidir?

a₁ = x, r = 6 ve a_n = y olduğuna göre, a_n = a₁r^{n – 1}    y = x.6^{n – 1}      6ⁿ = 6y/x ... (*)

S_n = a₁.(1 – rⁿ)/(1 – r) = x . (1 – 6ⁿ)/(1 – 6) = x . (1 – 6y/x)/(-5) = (6y – x)/5 dir.

SERİLER

A. TANIM

• (a_n) reel terimli bir dizi olsun.

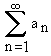
= a₁+a₂+a₃+ ...+a_n + ... sonsuz toplamına seri denir.

a_n’e serinin genel terimi denir.

Serinin ilk n teriminin toplamından oluşan S_n = a₁+a₂+a₃+ ...+a_n  toplamına serinin n. kısmi toplamı denir. (S_n) = (S1,...,S2,...,S₃,...,Sn,...) dizisine kısmi toplamlar dizisi denir.

a) (S_n) dizisi yakınsak ise 

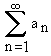
serisi de yakınsaktır ve serinin toplamı 

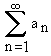
= lim S_n’ dir.

b) (S_n) dizisi ıraksak ise

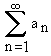
 seriside ıraksaktır.

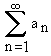
serisi yakınsak ise lim a_n = 0’dır. Bu ifadenin tersi doğru değildir.Yani, lim a_n = 0 iken

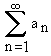
serisi yakınsak olmayabilir.

lim a_n≠0 ise  

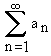
serisi ıraksaktır.

ÖRNEK

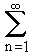
2ⁿ/5^-n serisi veriliyor. Serinin ıraksak olduğunu gösteriniz.

a_n = 2ⁿ/5^-n = 2ⁿ.5ⁿ = 10ⁿ dir. lim a_n = lim 10ⁿ = ¥dur. lim a_n ¹0 olduğuna göre seri ıraksaktır.

B. ARİTMETİK VE GEOMETRİK SERİLER

Aritmetik Seriler

(a_n) dizisi bir aritmetik dizi ise 

 
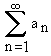
 serisine aritmetik seri denir. Aritmetik serinin kısmi toplamı S_n =n /2 (a₁+a₂)’dir. Aritmetik seri ıraksaktır.

ÖRNEK

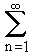
(n – 10)/20 serisi veriliyor. Serinin, aritmetik seri olduğunu gösteriniz. Serinin kısmi toplamını bulunuz. Serinin ıraksak olduğunu gösteriniz.

 Ɐn ∈N⁺ için d = a_{n +1} – a_n =(n+1-10)/20 – (n-10)/20 = 1/20 olduğu için seri aritmetik seridir.

a₁ = -9/20 ve a_n = (n – 10)/20 olduğuna göre, S_n =n/2(a₁+a_n) = n/2[-9/20 + (n –10)/20]

                                                                              =n(n – 19)/40 =  ∞   

olduğuna göre (S_n) kısmi toplamlar dizisi ıraksaktır. (S_n) kısmi toplamlar dizisi ıraksak olduğu için sorulan seri ıraksaktır.

1. Geometrik Seriler

(a_n) dizisi bir geometrik dizi ise 

 
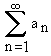
 serisine geometrik seri denir. Geometrik serinin kısmi toplamı S_n = a₁.(1-rⁿ)/(1-r)dir.

 a.  |r| < 1 ise seri yakınsaktır ve serinin toplamı:

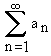
= a₁/(1-r)'dir.

 b. |r| ≥1  ise seri ıraksaktır.

ÖRNEK

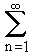
 3^1-n serisi veriliyor.

Serinin, geometrik seri olduğunu gösteriniz, serinin kısmi toplamını bulunuz, serinin yakınsak olduğunu gösteriniz, serinin toplamını bulunuz.

Ɐn ∈N⁺ için, r = (a_n+1)/a_n = 3^1-(n+1)/3^1-n = 1/3 olduğu için seri geometrik seridir.

a₁ = 1 ve r = 1/3 olduğuna göre,

S_n = 1 . [1 – (1/3)ⁿ]/(1 – 1/3) = 3/2[1 – (1/3)ⁿ] dir.

r = 1/3 olduğuna göre |r| = |1/3| = 1/3 < 1 dir. Bunu için seri yakınsaktır.

Seri yakınsak olduğuna göre toplamı

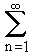
3^{1 – n} = a₁/(1 – r) = 1/(1 – 1/3) = 3/2 dir.