İHTİMALLER HESABININ AMACI ve TARİHÇESİ
İhtimal teorisi, tesadüfi olaylara egemen olan kanunları matematiksel metotlarla inceleyen bir bilimdir.
Bir deney aynı şartlar altında bir çok kez tekrar edildiğinde sonuçlar belli bir kurala bağlı olmaksızın her kez değişebiliyorsa, bu deneyin belirli bir sonucuna bağımlı olarak gerçekleşen (ya da gerçekleşmeyen) bir olaya tesadüfi olay denir.
ÖRNEK 1: Zar atma deneyinin altı değişik sonucu vardır. Deney tekrarlandığında hangi sonucun çıkacağını önceden belirleyen bir kural yoktur, sonuçlar tesadüfi olarak çıkar. “Zar 6 gelirse A kazanır” şeklindeki bir olay tesadüfi olaydır.
ÖRNEK 2: Ankara belediye otobüslerinden belli bir tanesinin bilet toplanan kutusu her gün akşam aynı saatte açılıp, içindeki biletler sayıldığında her gün değişik sayılar çıkar. Bilet sayıları tesadüfi olarak değişir. “Bilet sayısı belli bir miktarı aşarsa şoföre prim verilecektir” şeklindeki olay tesadüfidir.
ÖRNEK 3: Ankara’dan İstanbul’a uçan bir yolcu uçağı bu yolu her uçuşta tam aynı sürede almaz. Uçuş süresi tesadüfi olarak değişir. “Uçağın 5 dakika rötar yapması” olayı, tesadüfi olaydır.
ÖRNEK 4: 21 Şubat 1983 günü saat 16:30’da doğan Kemal 4 kg. doğmuştur; ama Ali başka anneden aynı anda 3,5 kg. doğmuştur. Yeni doğan bebeklerin vücut ağırlıkları gibi, boy uzunlukları, cinsiyetleri vb... vasıflar tesadüfi olarak değişir.
Bu örnekler ve daha nice benzerlerinde görüleceği gibi, bir çok doğal olaylar tesadüfi olaylardır. Kuşkusuz doğada tamamıyla belirli sonuçlar veren deneylere de pek çok örnekler gösterilebilir: “Taş bırakıldığında düşer”. Deney tekrar edildiğinde her kez taş düşer. Bu olayda tesadüfilik yoktur. Çünkü deneyin ne sonuç vereceğini belirleyen kural vardır, “o da Newton’un çekim kanunu” dur. Ama taşın düşeceği nokta aynı nokta olmayabilir, tesadüfi olarak değişir. “İnsan doğar yaşar, ölür”. Ölüm kesindir, tesadüfi değildir. Fakat ömür, yani yaşam süresi, tesadüfidir. Anlaşılan hemen her belirli olaya az çok tesadüfilik de eşlik ediyor. Şu var ki pozitif bilimlerde ve uygulamalı bilimlerde doğa olayına etki eden ikinci faktörler yani tesadüfi olarak değişen elemanlar genellikle ihmal edilir yalnızca birinci elemanlar dikkate alınır. Çünkü bunlar deney boyunca kontrol edilebilen değişkenlerdir. Birinci elemanlar problemin parametrelerini oluşturur. Parametreler, duruma göre değerler alan değişkenlerdir ama tesadüfi olarak değiş mezler. Meselâ, yatayla q açısı yapan bir eğik atışta merminin ilk hızı V0 ise, merminin düştüğü yerin uzaklığı d = f (q, V0 ) fonksiyonu ile belirtilebilir. Burada d uzaklığına etki eden birinci elemanlar 6 ve V0 hep aynı kalsa da atış tekrar edildiğinde mermi aynı noktaya düşmeyebilir. Bunun nedeni, olaya etki eden tesadüfi elemanlardır. Merminin düştüğü noktaların bir merkez etrafında yayılması, başka deyimle merkeze uzaklıkların değişimi tesadüfidir. Bu değişim hangi kanuna uyar? İşte ihtimal teorisinin uğraşı alanına giren bir örnek karşısındayız. d = f (q, V0) fonksiyonunu elde etmek mekanik biliminin uğraşı alanına girer. Demek ki tesadüfi olayların rol oynadığı problemlerin incelenmesi ve tesadüfi olayların bağlı olduğu kanunları ortaya koymak ihtimal teorisinin amacını teşkil eder.
Tesadüfi olaylara etki eden nedenlerin çokluğu ve karmaşıklığı bunların incelenmesi için özel metotları gerekli kılmıştır. Bu metotlar ihtimal teorisi içinde geliştirilmişlerdir. Pratikte deneyler göstermiştir ki, bir tesadüfi olayın gerçekleşmesi ya da gerçekleşmemesi pek çok sayıda gözlemlendiğinde, az çok bir kararlılık gösterir. Meselâ, Ankara doğum evinde yıllar boyunca tespit edilen erkek doğum oranının % 50’ye yakınsadığı kolaylıkla gözlemlenebilir. Demek ki tek başına bir tesadüfi olayın karmaşıklığına karşılık, bunların cümlesi için geçerli basit bir kanun elde edilebiliyor.
Öğrencilerin bir imtihandan aldığı notlar tesadüfi olarak değişir. Çok sayıda öğrencilerin aynı imtihandan aldığı notların bir merkezi puan etrafında yoğunlaştığını, az bir kısmının merkezden uzak çok düşük puanlar; gene az bir kısmının da merkezden uzak çok yüksek puanlar aldığını her zaman gözlemlemekteyiz. Bu notların dağılımı Normal kanuna ya da Gauss kanununa uyarlar. Normal kanun ilerdeki bir bölümde ayrıntılı olarak tanıtılacaktır.
İhtimal teorisi, metot olarak olayları tek tek değil toplu olarak inceleme metodunu kabul eder. Tek tek olayların özellikleri klâsik bilimsel metotlarla ortaya konurken ihtimal teorisinin metotlarından yararlanılabilir. Meselâ, Astronomi, Nükleer Fizik, Kimya, Biyoloji, Tıp, Veterinerlikte, Ekonomide, Planlama ve Programlamada, Askeri Operasyonlarda, Meteorolojide ihtimal metodlarına sık sık başvurulur.
İhtimal metotları, matematiksel metotlar yardımıyla ortaya çıkarılmış oldukları için ihtimal teorisi, matematiğin bir dalı olarak gözetilir. Bu nedenle ihtimal teorisi de matematiğin diğer dalları kadar mantıklı ve kesin sonuçlar verir.
Özetle ihtimal teorisi, matematiğin diğer dalları gibi, uygulama ihtiyaçlarından doğmuştur.
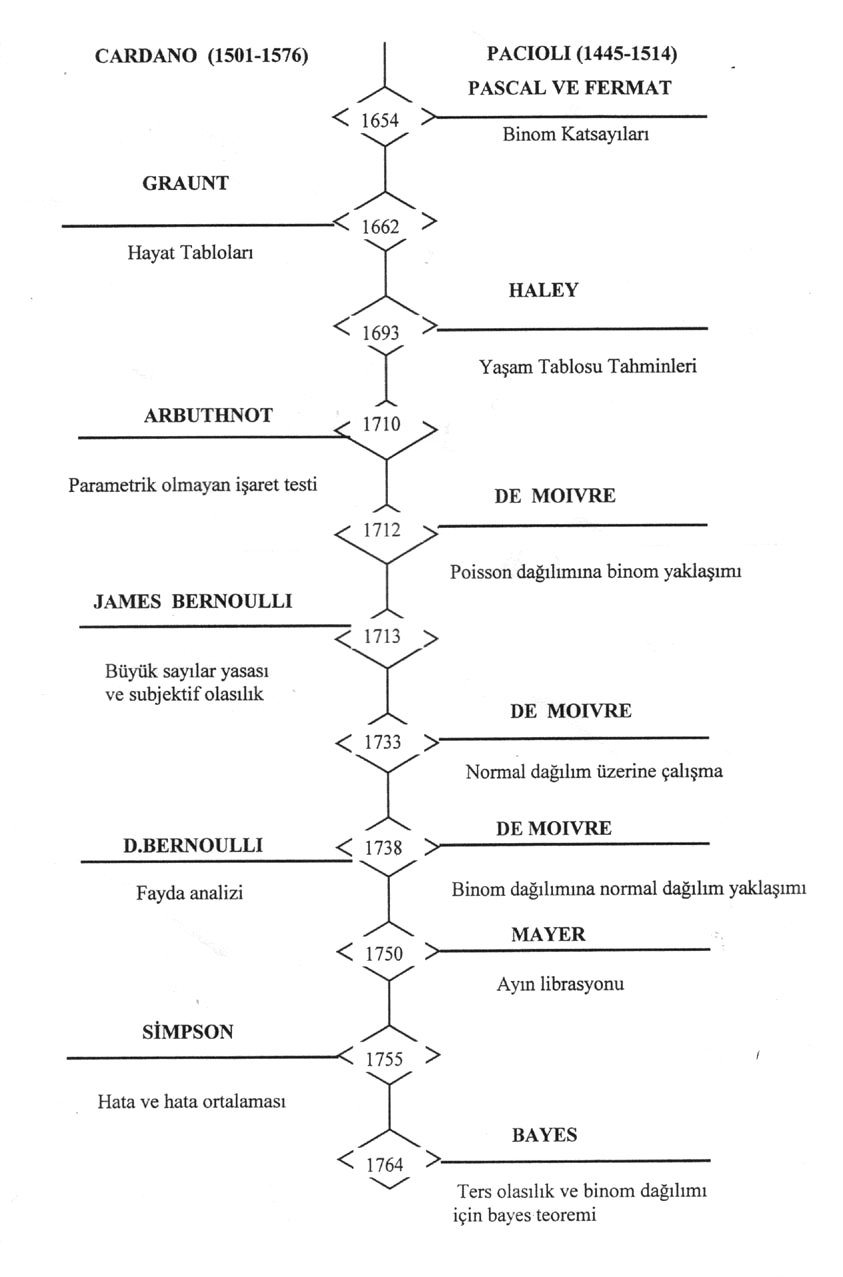
Tesadüfi olaylara ilişkin problemlerin sistematik biçimde incelenmesine XVII.’ci yüzyılda başlanmıştır. Bu yüzyıl başlarında ünlü fizik bilgini Galile fiziksel çoklukların ölçüm hatalarını incelemeye girişmiş ve bunların tesadüfi olarak değiştiğini kabul ederek, hataların ihtimallerini hesaplamıştır. Bu yüzyılda bir yandan da sigorta hesaplarının ilk defa yapıldığı göze çarpıyor. Bu hesaplar, tesadüfi olaylara egemen olan kanunların analizine dayandırılıyordu. Tesadüfi olayları analiz etmeye yarayan bir matematiksel araç bulma zorunluluğu kendini hissettirmişti. Bunun için de önce, en basit tesadüfi olayları incelemek gerekiyordu. Sistematik inceleme, şans oyunları ile başladı. XVI. ve XVII. Asırlarda, şans oyunları özellikle zengin şahıslar arasında yaygındı ve olasılık gerektiren pek çok sorular zamanın çok iyi bilinen matematikçilerinden Cardano, Galile, Pascal, Fermat, Leibnitz ve Bernoulli’ye kart çekmeyi, zar atışını ve çoğu kez karışık kural gruplarını içine alırdı kumarcılar kazanmalarını en yüksek düzeye çıkartmak için gereksindikleri en iyi stratejiyi kullanmayı arzu ettiler. Gerçekten şans oyunları, tesadüfi olaylara, çok basit ve anlaşılması kolay modeller oluştururlar. Bu nedenle bugün de ders kitaplarında bunlardan yararlanılır.
Modern anlamda ihtimal teorisinin doğuşu 1650’ye doğru Fermat (1601-1665), Pascal (1623 -1662) ve Huygens (1629 -1695)’in oyunlar teorisine ilişkin çalışmaları sonucunda gerçekleşmiştir. Bu çalışmalarda yavaş yavaş ihtimaller hesabının önemli kavramlarına ve “matematiksel umut” kavramına rastlanıyor. İhtimal hesaplarının metotları öncelikle sigorta problemlerinde kullanılmıştı. XVII. ci yüzyılın sonlarından itibaren sigorta hesapları bilimsel metotlara dayandırılmış bulunuyordu. Bir süre sonra ihtimal teorisi diğer alanlara da girdi.
Jacob Bernouilli (1654 - 1705)’nin çalışmaları ihtimal teorisini bir adım daha ileri götürdü. İhtimal teorisinin temel kanunlarından biri olan “Büyük Sayılar Kanunu”nu ilk defa J. Bernouilli ispat etmiştir. Bernouilli ilk kez bir olayın ihtimalini bu olayın frekansının limiti olarak tanımlamıştır.
İhtimal teorisinin gelişiminde bir başka adım De Moivre (1667 - 1754) ile başlar. Normal kanunu ya da Gauss kanununu, en basit hal için, ilk kez Moivre bulmuş ve ispatını vermiştir.
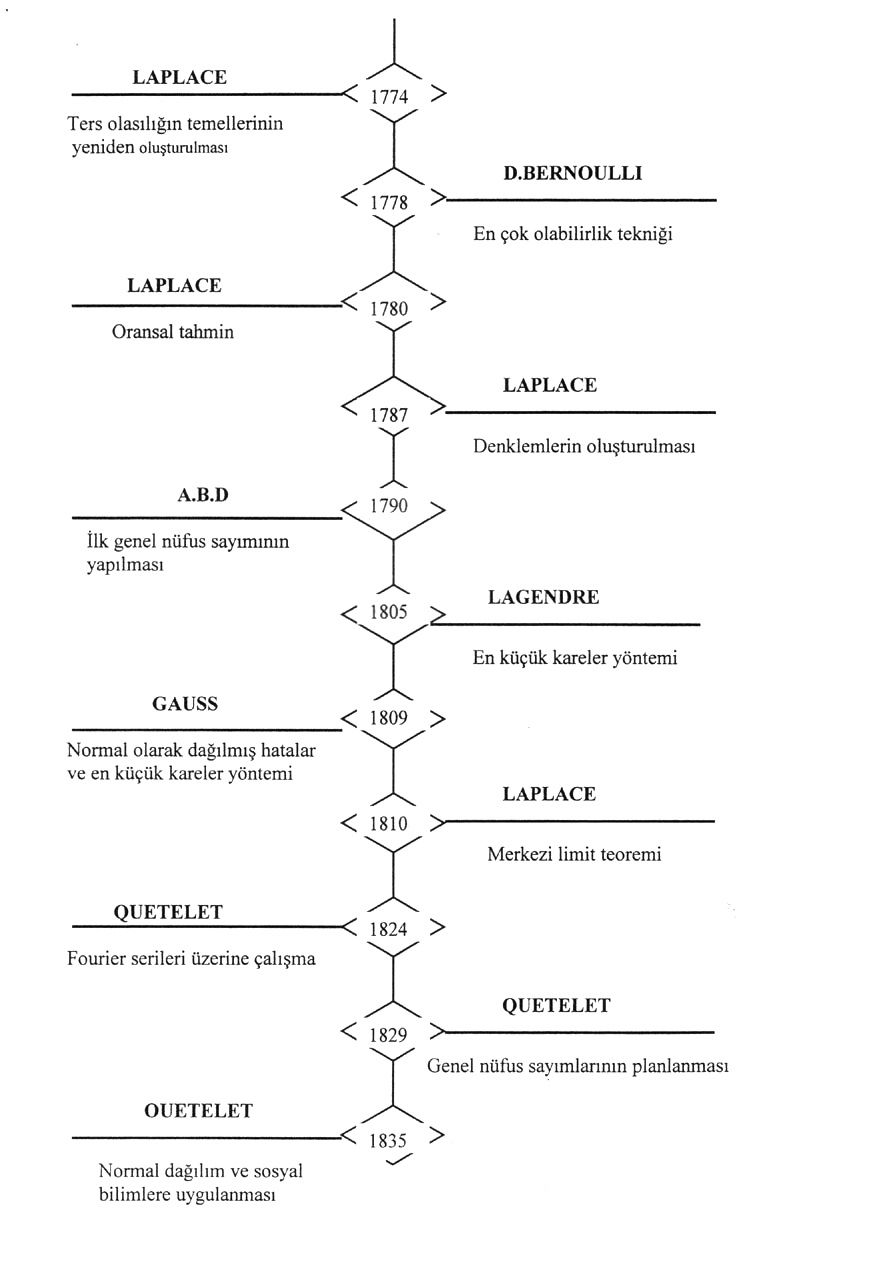
Sonra, Laplace (1749 -1827), Gauss (1777 -1855), Poisson (1781 -1840) un çalışmaları gelir. İhtimal teorisinin temel taşlarından biri olan “Merkezi Limit Teoremi” (Moivre - Laplace Teoremi) ilk kez Laplace tarafından ispat edilmiş ve bir çok dikkate değer uygulamaları yapılmıştır. Özellikle, gözlem ve ölçüm hatalarına ilişkin uygulamalar üzerinde durulmuştur. Gauss, Normal Kanunu daha ciddi bir biçimde ortaya koymuş “En Küçük Kareler Yöntemini” bulmuştur. Poisson, Özellikle uygulama alanı çok geniş olan teorik yönüyle de gayet ilginç olan dağılım kanunlarından birini “Poisson Dağılım Kanunu” nu bulmuştur.
XVIII. ci yüzyıl ve XIX. cu yüzyılın başları, ihtimal teorisinin yoğun biçimde gelişme gösterdiği bir dönemdir. Bu dönemde ihtimal hesapları bilim adamları arasında adeta moda olmuştur. Hukuk problemlerine, tarih araştırmalarına, politikaya, hatta teolojiye bile uygulanmaya girişilmişti. Tüm düşünce ve muhakemelerde, belli ihtimal kabulünden hareketle yola çıkılıyordu. Meselâ, hukuk problemlerinde, kabul ediliyordu ki insanlar aynı ihtimalle yalan veya doğru söyler. Bir sosyal problem, basit bir aritmetik problemi gibi çözülüyordu. Aşikâr ki tüm bu girişimler başarısızlığa mahkumdu ve bilimsel gelişmede olumlu bir rol oynayamazdı. Nitekim XX. ci yüzyıla doğru artık ihtimal teorisi ile varılan sonuçlara şüphe ile bakılıyor ve güvenilmiyordu. Geniş bir zümrenin gözünde, ihtimal hesapları bir tür matematiksel eğlence gibi görülüyor ve ciddiye alınmıyordu.
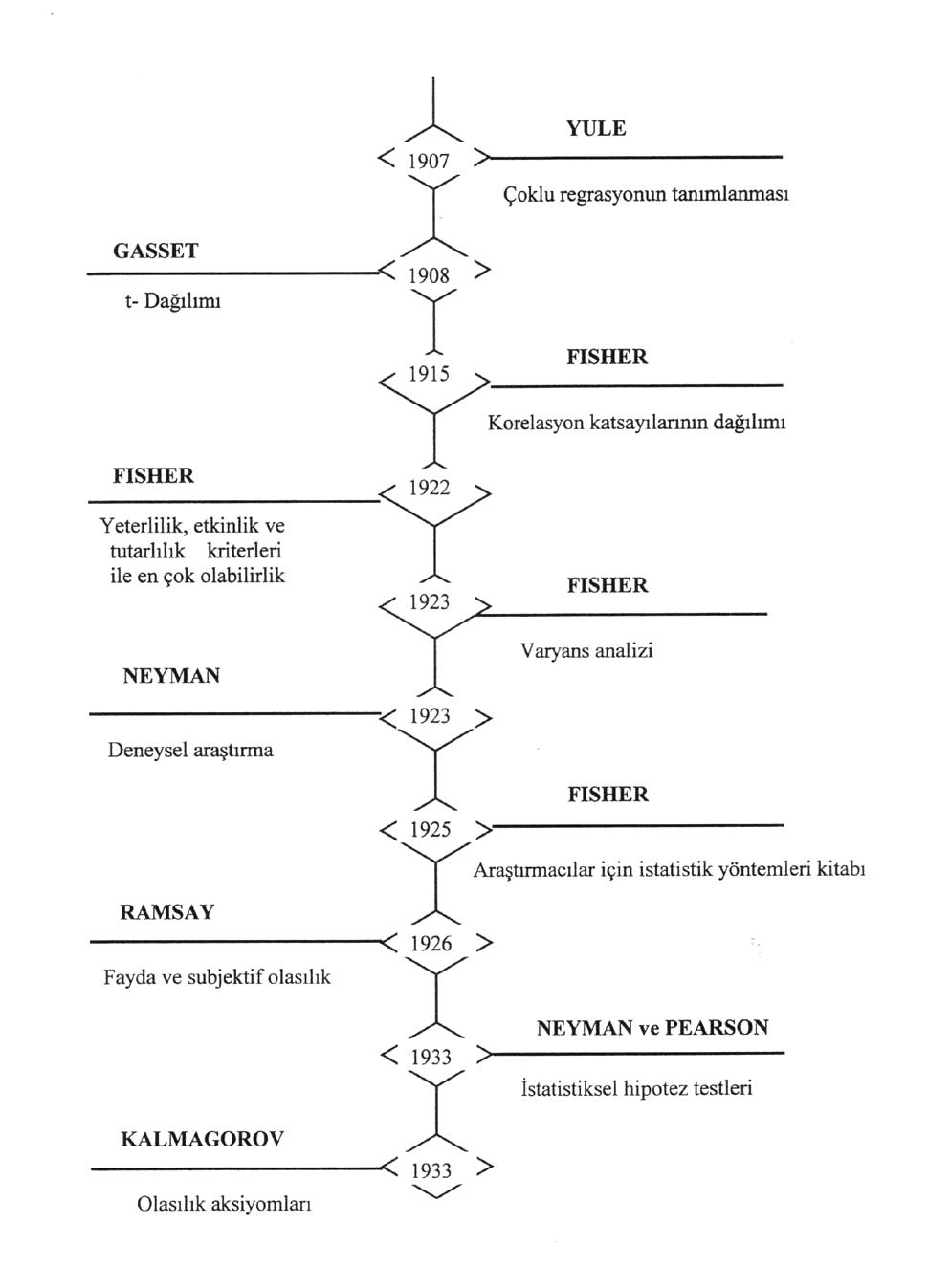
Ancak, Tchebychev (1821-1891) ve Markov (l 856 -1922) un çalışmaları ihtimal teorisinin gelişmesine yeniden hız kazandırdı, özellikle Markov Tesadüfi Süreçler teorisinin temelini attı.
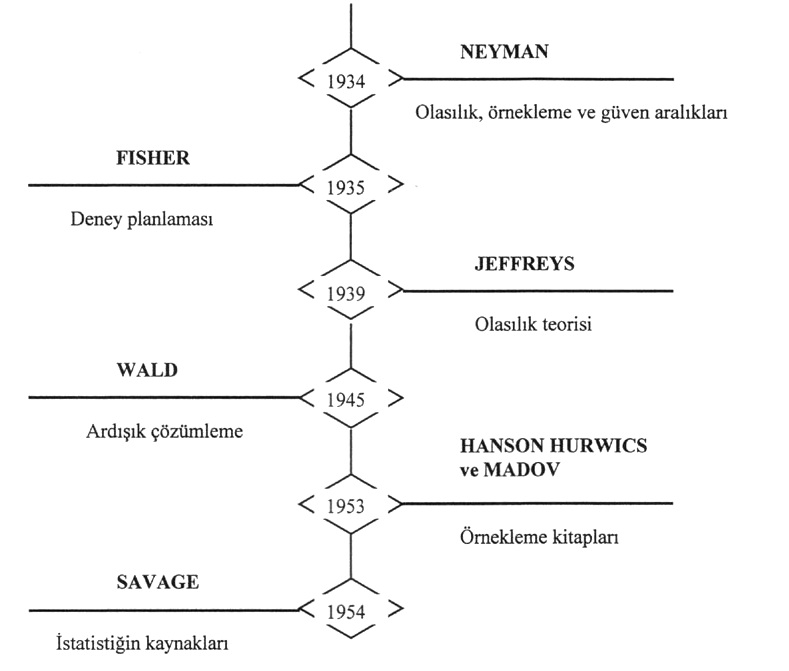
“XX. ci yüzyılda” ihtimal Teorisi modern bir aksiyomatik kuruluşa kavuştu. Çağımızda Tesadüfi Süreçler’e ilişkin problemlere büyük ilgi gösterilmektedir. Bu alanda emeği geçen başlıca bilim adamları arasında N. Wiener, W. Feller, J. Dobb, A. Kolmogorov, R. Fisher, J. Nevmann ve H. Gramer ’in isimlerini anabiliriz.


Yorumlar4
buda görsel ispatı
http://www.merasimsek.com/index.php?option=com_content&task=view&id=39&Itemid=28
1+2+3+...+n=(n).(n+1)/2
ıspat
1+2+3+....+n=x olsun şimdide geriden yazalım
n+(n-1)+(n-2)+...+1=x
taraf tarafa toplarsak
(n+1)+(n+1)+(n+1)+...+(n+1)=2x
(n tane)
n.(n+1)=2x
n(n+1)/2 =x
ıspat tamamlanmış olur
http://forum.shiftdelete.net/konu-disi/61398-gaus-tok-etme-yontemi.html
bu forumda aynı istekte bulunan sizmiydiniz?
size matematiksel ispatımı gerekiyor
Gaus kanununun ispatı lazım bir ödevim için. nasıl ulaşabilirim?
Yorumlarınızı Bekliyoruz
Yorum Yazın
Yorum Yapın