Türev Konusu
Türevin Anlamı
TÜREVİN FİZİKSEL ANLAMI
Bir hareketlinin t saatte kaç km yol aldığı, s(t) fonksiyonu ile verilsin.
TÜREVİN GEOMETRİK ANLAMI,
y = f(x) fonksiyonunun A(x0, y0) noktasındaki teğetinin Ox ekseniyle yaptığı pozitif yönlü açının ölçüsü a olsun. Teğetin eğimi, tana ya eşit olduğu için:
m = tana dır.
y = f(x) fonksiyonunun x = x0 daki türevi A(x0, y0) noktasındaki teğetinin eğimine eşittir.
f’(x0) = m = tana dır.
Eğimi m olan ve A(x0, y0) noktasından geçen doğrunun denklemi, olduğu için, y = f(x) eğrisinin A(x0, y0) noktasındaki teğetinin denklemi,
Birbirine dik olan doğruların eğimleri çarpımı – 1 olduğu için, y = f(x) eğrisinin A(x0, y0) noktasındaki normalinin eğimi:
Buna bağlı olarak, y = f(x) eğrisinin A(x0, y0) noktasındaki normalinin denklemi,
ARTAN ve AZALAN FONKSİYONLAR
x1 < x2 iken f(x1) < f(x2) ise f(x) fonksiyonu artandır.
x1 < x2 iken f(x1) > f(x2) ise f(x) fonksiyonu azalandır.
Artan fonksiyonun türevi daima pozitiftir. Bu ifadenin tersi de doğrudur. Azalan fonksiyonun türevi daima negatiftir. Bu ifadenin tersi de doğrudur.
Her x1, x2 için, f(x1) = f(x2) ise f(x) fonksiyonu sabittir.
EKSTREMUM DEĞERLER ve BUNLARIN TÜREVLE İLİŞKİSİ
Ekstremum Noktalar
P noktası yerel maksimum noktasıdır.
Yerel maksimumların en büyüğü de mutlak maksimum noktasıdır.
r noktası yerel minimum noktasıdır.
Yerel minimumların en büyüğü de mutlak minimum noktasıdır.
Fonksiyon maksimum ve minimum değerlerinin hepsine birden, fonksiyonun yerel ekstremum değerleri denir.
Fonksiyon ekstremum noktalarda türevli ise, türevi sıfırdır. Tersi her zaman doğru değildir.
Birinci Türevden Yararlanarak Ekstremum Noktaların Belirlenmesi
f’(x0-h)>0
f’(x0)=0
f’(x0+h)<0
h > 0 olmak üzere, ise y = f(x) fonksiyonu x = x0 da yerel maksimuma sahiptir. Yerel maksimum değer, f(x0) dır.
f’(x0-h)<0
f’(x0)=0
f’(x0+h)>0
h > 0 olmak üzere, ise y = f(x) fonksiyonu x = x0 da yerel minimuma sahiptir. Yerel minimum değer, f(x0) dır.
Yukarıda verilen tanım türevlenebilir fonksiyonlar için doğrudur. Ancak y = f(x) fonksiyonu x = x0 da türevsiz olduğu hâlde x = x0 da yerel maksimuma ya da yerel minimuma sahip olabilir.
Birinci türevin sıfır olduğu noktada, türevin işareti değişiyorsa yerel maksimuma ya da yerel minimuma sahiptir. Fonksiyonun türevinin işaret tablosunda soldan sağa doğru, işaretin – den + ya geçtiği noktada yerel minimum; işaretin + dan – ye geçtiği noktada yerel maksimum vardır.
Birinci Türevden Yararlanarak Ekstremum Noktaların Belirlenmesi
f’(x0-h)>0
f’(x0)=0
f’(x0+h)<0
h > 0 olmak üzere, ise y = f(x) fonksiyonu x = x0 da yerel maksimuma sahiptir. Yerel maksimum değer, f(x0) dır.
f’(x0-h)<0
f’(x0)=0
f’(x0+h)>0
h > 0 olmak üzere, ise y = f(x) fonksiyonu x = x0 da yerel minimuma sahiptir. Yerel minimum değer, f(x0) dır.
Yukarıda verilen tanım türevlenebilir fonksiyonlar için doğrudur. Ancak y = f(x) fonksiyonu x = x0 da türevsiz olduğu hâlde x = x0 da yerel maksimuma ya da yerel minimuma sahip olabilir.
Birinci türevin sıfır olduğu noktada, türevin işareti değişiyorsa yerel maksimuma ya da yerel minimuma sahiptir. Fonksiyonun türevinin işaret tablosunda soldan sağa doğru, işaretin – den + ya geçtiği noktada yerel minimum; işaretin + dan – ye geçtiği noktada yerel maksimum vardır.
İkinci Türevden Yararlanarak Ekstremum Noktaların Belirlenmesi
ise f(x) fonksiyonu x = x0 da yerel maksimuma sahiptir. Yerel maksimum değeri, f(x0) dır
ise f(x) fonksiyonu x = x0 da yerel minimuma sahiptir. Yerel minimum değeri, f(x0) dır.
İKİNCİ TÜREVİN GEOMETRİK ANLAMI
Konveks Eğriler
[a, b] aralığında f ”(x) > 0 ise, f nin grafiği olan eğri konveks (dış bükey) dir. Diğer bir ifadeyle, bükülme yönü yukarı doğrudur. Eğri, teğetlerinin yukarısındadır.
Aşağıdaki grafiklerde verilen eğrilerin üçü de konvekstir.
Konkav Eğriler
[a, b] aralığında f ”(x) < 0 ise, f nin grafiği olan eğri konkav (iç bükey) dir. Diğer bir ifadeyle, bükülme yönü aşağı doğrudur. Eğri, teğetlerinin altındadır.
Aşağıdaki grafiklerde verilen eğrilerin üçü de konkavdır.
Dönüm (büküm) Noktası
f, sürekli olmak üzere, fonksiyonun konvekslikten konkavlığa ya da konkavlıktan konveksliğe geçtiği noktaya dönüm (büküm) noktası denir.
Diğer bir ifadeyle, f nin grafiği olan eğrinin, eğrilik yönünün değiştiği noktaya, dönüm (büküm) noktası denir.
x = x0 noktasının dönüm noktası olması, x = x0 da ikinci türevin olmasını garanti etmez. Yani, dönüm noktasında türev tanımlı olmayabilir. x = x0 ın ikinci türevin kökü olması, x = x0 ın dönüm noktası olmasını garanti etmez. Dönüm noktasında ikinci türevin işaret değiştirmesi gerekir. x = x0 dönüm noktası ve bu noktada ikinci türev tanımlı ise, ikinci türev sıfırdır.
y = f(x) fonksiyonunun grafiğine göre c büküm noktasının apsisi ise aşağıdakiler söylenebilir.
- (a < x < b ve d < x < e ) için fonksiyon azalandır. Bu aralıkta f ‘(x) < 0 dır.
- b < x < d için fonksiyon artandır. Bu aralıkta f ‘(x) > 0 dır.
- a < x < c için f ”(x) > 0 dır.
- x = b de f(x) in yerel minimumu, x = d de f(x) in yerel maksimumu vardır. Bu nedenle, f ‘(b) = 0 ve f ‘(d) = 0 dır.
- x = c de f(x) in dönüm noktası vardır. Bu nedenle, f ”(c) = 0 dır.
Türev
a, b birer reel sayı olmak üzere,
eşitliği de yazılabilir.
SAĞDAN VE SOLDAN TÜREV
fonksiyonu için,
limiti varsa bu limite f fonksiyonunun x = a daki sağdan türevi denir. Ve
biçiminde gösterilir. Benzer şekilde,
limiti varsa bu limite f fonksiyonunun x = a daki soldan türevi denir. Ve
biçiminde gösterilir.
f fonksiyonunun, x = a daki sağdan türevi soldan türevine eşit ise f nin x = a da türevi vardır (ve bulunan bu limit değerleri, o noktadaki türeve eşittir). Aksi takdirde türevi yoktur.
- f ‘(a+) = f’(a–) ise f fonksiyonunun x = a da türevi vardır.
- f fonksiyonunun x = a da türevi varsa f fonksiyonu x = a da süreklidir.
- f fonksiyonu, x = a da sürekli olduğu hâlde, o noktada türeve sahip olmayabilir.
- f fonksiyonu x = a da sürekli değilse türevli de değildir.
Bir fonksiyonun, bir noktada türevinin olması için gerek koşul, o noktada sürekliliktir. Ancak bu, o noktada türevin olması için yeterli değildir.
TÜREV ALMA KURALLARI
in Türevi
c Sabit Sayısının Türevi
c × f(x) in Türevi
Toplamın Türevi
Farkın Türevi
Çarpımın Türevi
Bölümün Türevi
Mutlak Değer Fonksiyonunun Türevi
f(a) = 0 ise fonksiyonun bu noktada türevi olabilir ya da olmayabilir. Bunu araştırmak için fonksiyonun sağdan ve soldan türevlerine bakılır. Sağdan ve soldan türevler eşit ise fonksiyon bu noktada türevlidir. Aksi hâlde türevli değildir.
Mutlak değer fonksiyonu tek katlı köklerde köşe (uç) oluşturur. Köşe (uç) noktalarda türev yoktur. Çift katlı köklerde köşe (uç) oluşmaz. Bunun için, çift katlı köklerde türev vardır ve sıfırdır.
f’(2) gösterimi [f(2)’ gösterimi ile karıştırılmamalıdır. Aynı değildir. Çünkü f’(2) gösterimi, fonksiyonun türevinin, yani f ’(x) in x = 2 için değeridir.[f(2)]’ gösterimi, fonksiyonun x = 2 için değerinin (Yani, bir reel sayının) türevidir. [f(2)]’ = 0 dır.
Parametrik Olarak Verilen Fonksiyonların Türevi
g ve h iki fonksiyon olmak üzere
y = g(t)
x = h(t)
denklemleri ile de belirtilebilir. Burada t ye parametre denir.
Bazen y = g(t) ve x = h(t) denklemlerinden t yok edilerek y = f(x) şeklinde bir denklem elde edilebilir. Ancak bu her zaman mümkün olmayabilir.
Bu durumda,
y = g(t), x = h(t) parametrik denklemleriyle verilen y = f(x) fonksiyonunun türevi aşağıda verilen kural yardımıyla bulunur.
y = f(x) in türevi
f’(x) in türevi olan
y = f(x) in ikinci mertebeden türevi denir. Benzer şekilde,
f: birebir ve örten bir fonksiyon ise f(x) in tersi olan fonksiyon bulunur. Sonra türev alınır. Bunun zor olduğu durumlarda ters fonksiyonun türevi şöyle alınır.
Ters trigonometrik fonksiyonların türevinin bulunmasında şu formüller kullanılabilir.
Türev ile İlgili Yazılar
İspatlarıyla Türev Alma Kuralları
Türev , diğer sayı kümeleri üzerindeki fonksiyonlar için genellenmiş olmasına rağmen öncelikle reel değerli, yani reel sayılardan reel sayılara giden tek değişkenli fonksiyonlar için tanımlanmış, kabaca bir fonksiyonun grafiğine çizilen teğetin eğimini hesaplama tekniğidir.
Bir f fonksiyonunun a noktasındaki türevi
-
 =
= -
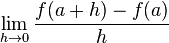
limiti olarak tanımlanır. Bu limitin temsil ettiği oran aşağıdaki grafikte gösterilmiştir.
