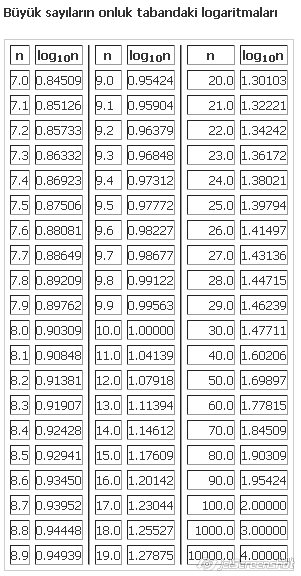
Logaritma Cetveli
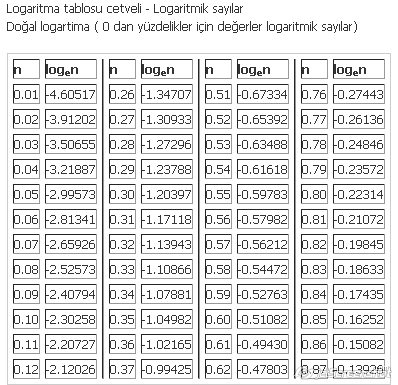
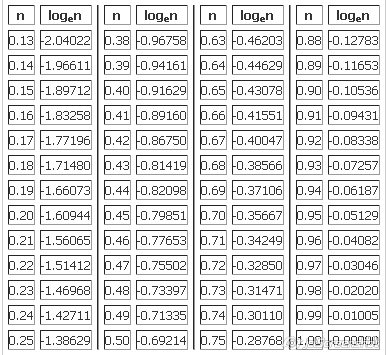
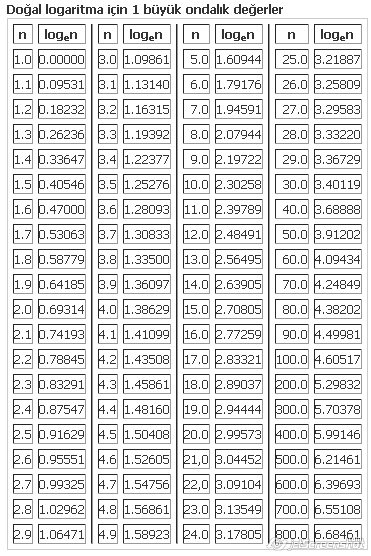
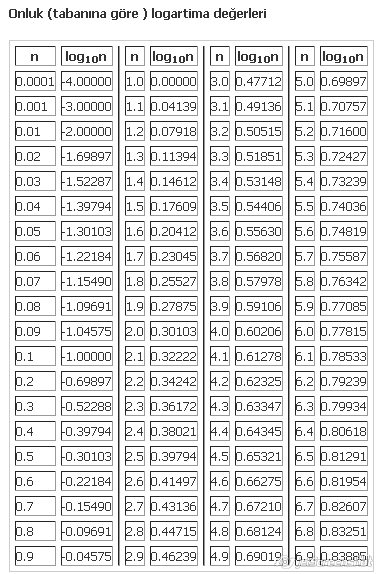
Logaritma cetveli logaritmik kavramların bulunduğu, logaritmik derecelerin karşılığı sayıları gösteren bir cetveldir. Çok karmaşık olan bu cetveli ezbere bilinmesinin imkânı yoktur. Zaten matematikçiler de ezbere bilmezler…


Logaritma 17. yüzyılın başında hesapları hızlandırmak için yapılan bir buluştur. 300 yıldan daha uzun bir zaman, temel bir hesap metodu olmuştur. 19. yüzyılda masa hesap makinalarının doğuşu ve yirminci yüzyılda elektronik hesap makinalarının ortaya çıkışı, logaritmaya olan ihtiyacı azaltmıştır. Ancak logaritmik fonksiyonların teorik ve uygulamalı matematikte özel bir yeri vardır.
Logaritma, birbirinden habersiz çalışan iki kişi tarafından keşfedilmiştir. Bunlar; 1614'te İskoçyalı John Napier ve 1620'de İsviçreli Joost Bürgi'dir.
Logaritma üzerinde önemli çalışmaları olan bir Türk bilgini de Gelenbevi İsmail Efendi'dir. Kendisi büyük bir matematikçi olup, mantıkla da uğraşmıştır. 1730-1790 yıllarında yaşayan bu büyük alimin Logaritma Risalesi isimli çok açık, anlaşılır yazılmış bir eseri mevcuttur.
Logaritmayı açıklamak için 2·2·2= 8 ifadesine bakalım. Bu 2³ = 8 olarak kısaca yazılabilir. Bu örnekte 3, 8'in 2 tabanına göre logaritması denir. Buradan çıkan sonuç log28=3 'dur. Başka bir örnek, 2·2·2·2 = 16 ve 24 = 16 yazılırsa, burada 4, 16'nın 2 tabanına göre logaritmasıdır. Yani log216=4 'tür. Genel olarak bx= N ifadesinde N'nin b tabanına göre logaritması, x'tir. Her ne kadar her pozitif sayı taban olarak kullanılırsa da genel olarak logaritma 10 ve e (yaklaşık, 2,718281828) tabanına göre hesaplanır.
Eğer taban olarak yaklaşık 2,718281828 olan e sayısı alınırsa, bu logaritma doğal logaritma veya keşfeden John Napier'e atfen Napier logaritması olarak da isimlendirilir. logeN yerine ln N ifadesi kullanılır. Mesela, ln 2 yaklaşık olarak 0,6932'dir. Doğal logaritma genel olarak, ilmi kanunların ifadesinde sık sık ortaya çıkar.
Adi ve doğal logaritmalar birbirleri ile alakalı olup, az hatalı bir çevirme yapılmak isteniyorsa, doğal logaritma, adi logaritmaya 0,4343 sayısı ile çarparak çevrilebilir.
Adi ve doğal logaritmaların dışında herhangi pozitif bir reel sayı tabanına göre de logaritma kullanılır. Ancak negatif sayıların hiçbir tabana göre logaritmasının olmayacağı açıktır.
Üslü olarak verilen bazi ifadelerin gerçek degerlerini, dogrudan dogruya bulmak, matematik yönünden yapilmasi zor bir islemdir. Kaynaklar, bu tür, birtakim hesaplamalari, kolaylikla yapilmasini saglayan, logaritmayi ilk kullanani, John Napier (1550 - 1617); oldugunu göstermekte.
John Napier tarafindan, bu konuda "Minifici Logaritmorum Canonis Descripto" (bir logaritma cetveli tanimi ve iki ayri trigonometri ile bütün matematik hesaplarinda kolay ve çabuk kullanilmasina genel açiklamasi); adli, zamanin bilim dili olan Latince olarak kaleme alinmis eser, ilk kez 1614 yilinda Edinburg sehrinde yayinlandi. Böylece logaritma adini da John Napier koymustur.
Bir logaritma çizelgesinin hazirlanmasinda, taban olarak 1 den büyük sayi seçilebilir. Napier, çizelgesini (e); tabanina göre hazirlamistir. Fakat çizelgeyi tamamladiktan sonra, (e); sayisini almakla, zor bir sistem ortaya koydugunu, uygulamasi sirasinda farkina vardi. Daha sonraki yillarda, 10 tabanli, yeni bir logaritma sisteminin hesaplama islerinde büyük kolayliklar saglayabilecegini düsündü. Fakat, bu yeni sisteme ait, düsündügü temel ilkeleri, bizzat ortaya koyamadan öldü. Ömrünün son günlerinde, arkadasi olan, Ingiliz matematikçi ve astronom Henri Briggs'ten (1551 - 1630); düsüncelerinin tamamlanmasini istedi.
Henri Biggs, bu istege uyarak, 10 tabanina göre, bir logaritma cetveli hazirlayarak, 1617 yilinda yayimlamistir. Bu eser, 1'den 1000'e kadar olan sayilarin 14 ondalikli logaritmalarini gösterir. Henri Briggs, ilk logaritma cetvellerinin yayimindan 7 yil sonra, yani 1624 yilinda; önceleri, 1'den 20.000'e daha sonra da, 90.000'den 100.000'e kadar olan sayilarin 14 ondalikli logaritmalarini kapsayan Logaritmik Aritmetik adli bir eser daha yayimladi.
Daha sonra, Hollandali matematikçi Adrien Vlacq, Henry Briggs'ten eksik kalan, 20.000'den 90.000'a kadar olan sayilarin logaritmik degerlerini hesap etti ve cetvellerini 1626 yilinda, Briggs' in adi altinda, Goude'de yayimladi. Bu yeni çizelgeler, 10 ondalikli olup, 1'den 1.000.000'a kadar sayilan , ve 0 dereceden 90 dereceye kadar olan açilarin, 1'er açi dakikasi aralikli olarak, için sinüs, tanjant ve sekantin logaritma degerlerini kapsiyordu. Ayrica, her biri 10" için, sinüs ve tanjantin logaritmalarina iliskin bir çizelge yayimlandi.Logaritma cetvelleri üzerine eser hazirlayanlar, Adrien Vlacq' in bu eserini temel kabul ederler


Yorumlar8
çok sacma
log 5 tabanında 2 nedir arkadaşlar ve nasıl bulcam değerini anlatırsannız sevinirm
nasl yani anlamadım güzel anlatmamışlar:)
off istediğim yok logaritma cetveli acilllllll........
güzelll
Yorumlarınızı Bekliyoruz
Yorum Yazın
Yorum Yapın