Eski Mısırlılar
Sık sık yapılan ölçümler gösterdi ki çapı üç kat aşan çapın dokuzda biri oranındadır. Bunu mısırlı bir katip olan Ahmes tarafından MÖ 1650 de yazılan ünlü Rhind Papirüsü’ne dayanarak söylüyoruz. Buna göre eğer biz bir dairenin çapının dokuzda sekiz uzunluğunda kenarları olan bir kare yaparsak bu karenin alanı dairenin alanına eşit olacaktır. Bu noktada sizin de fark edebileceğiniz gibi çevrenin çapa olan oranını bulmak için hiçbir neden yoktu. Asıl konu ise klasik araçları kullanarak (belirtilmemiş bir düz kenar ve bir çift pergel) belirli bir daireyle aynı alana sahip bir kare oluşturabilmekti. Bu eski çağların en popüler üç probleminden biri haline geldi.
İşte şimdi bizler de onların yaptığı çalışmayı taklit edeceğiz. d çaplı bir daireyle işe başlayacağız.yukarıda anlatılanlara göre karenin bir kenarı 8d/9 olacak.
Milattan önce π
1936 yılında Babil kenti yakınlarında bulunan Susa’da yapılan kazılarda bazı matematiksel içerikli tabletler bulundu. Bu tabletlerin birinde normal bir altıgenin çevresinin bu altıgenin dış teğet dairenin çevresine olan oranı karşılaştırılıyordu. İşte bu tablet sayesinde günümüz matematikçileri Babillilerin πdeğerini 3 tam 1/8= 3,125 olarak hesapladıkları sonucuna vardılar.
Bir dairenin çevresinin çapına olan oranının (π) tarihsel gelişiminde yolculuk ederken MÖ 550 yılında yazılmış olan Eski Ahit’teki 1. Krallar ve 2. Tarihler bölümünde Kral Süleyman’ın havuzunun tanımı yapılırken π’ye 3 değerinin verildiği sonucuna varıyoruz.
Arşimed’in katkıları
Matematik tarihine belki de ilk önemli katkıda bulunanlardan biri Archimedes’tir. Archimedes MÖ 287 yılında astronom Phidas’ın oğlu olarak Sicilya’da dünyaya geldi. Bir süre Öklid’in izinden gidenlerle mısırda çalıştı.
Archimedes’in Measurement of the Circle (Dairenin Ölçülmesi) adlı eserinde π’nin tarihsel gelişiminde önemli bir rol oynayan daireyle ilgili 3 sav bulunmaktadır. Bu üç savın her birini kısa açıklamalarla sizlere sunmaya çalışacağız.
1. Dairenin alanı dik kenarları dairenin yarıçapı ve çevresine eşit olan bir dik üçgenin alanına eşittir.

3. Bir dairenin çevresi kendi çapından 3 tam 1/7 kere daha küçüktür; ancak çaptan 3 tam 10/71 kere daha büyüktür.
Archimedes’in yaptığı şey belirli bir dairenin içine düzgün bir altıgen çizmek ve daha sonra yine bir altıgenle bu dairenin dış teğetini almaktan ibaretti. Böyle yaparak her iki altıgenin de alanlarını bula biliyor ve böylece dairenin alanının bu altıgenlerin alanlarının arasında bir yerde olduğunu biliyordu.
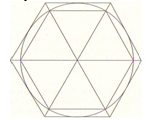
Archimedes aynı işlemi 12 kenarlı düzgün çokgenlerde tekrar etti ve bunu her yapışında her birinin alanını yeniden hesapladı. Böylece fark etti ki dairenin alanı bu değerler arasında bir yerde olmalıydı. Daha sonra modern bir dille ifade edersek bu değerler arasında sıkışıp kalmış olmalıydı. Sonunda Archimedes πdeğerinin 3 tam 10/71 den büyük, 3 tam 1/7 den küçük olduğu sonucuna vardı.
Milattan Sonraki Yıllar
Şimdi de büyük bir gökbilimci, coğrafyacı ve matematikçi olan MS 150 yılında Algamest adında astronomi alanında yazılan bilimsel incelemenin yazarı olan ve genellikle Ptolemy aşağıdaki sonucu elde etmek için altmışlık sistemi kullandı.
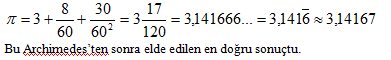
Rönesans Başlangıcı
Leonardo Pisano (1170-1250) ilk olarak 1202 de yayımlanan ünlü kitabı Liber Abaci’de bugün kullandığımız Hint sayı sisteminden bahsetmiştir. Batı Avrupa’da bu sistemden yazılı olarak bahseden kişiydi. 1223 yılında doksan altı kenarlı düzgün bir çokgeni kullanarak hesapladığı πdeğerinin de içinde bulunduğu Practica Geometriae adlı kitabını yazdı. Bu kitaptaki değer aşağıdaki gibiydi.
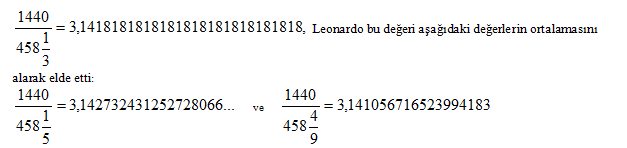
On Yedinci Yüzyıl
π değerinin en doğru bulmak için yola çıkan Alman matematikçi Ludolph van Ceulen (1546-1610) 1596 yılında π’yi 20 ondalık basamaklı bir sayı olarak hesapladı.bu sonucuna 60.233=515396075520 kenarlı iç ve dış teğetleri alınmış düzgün bir çokgenin çevresinden ulaştı.
Cambridge ve Oxford üniversitelerinde matematik profesörlüğü yapmış olan John Wallis’in (1616-1703) 1655 yılında yayımladığı Arithmetica İnfinitorum adlı kitabında πiçin bir formül öne sürüyordu:
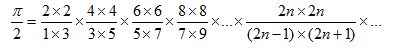
Yani terimlerin sayısı arttıkça 2 ile çarpmak bizi bu sayının değerine daha da yaklaştırır.
On Sekizinci Yüzyıl- π’nin Günümüzdeki İsmini Aldığı Yıllar
1706 yılında Synopsis (Matematiğe Yeni Bir Giriş) adlı kitabında William Jones (1675-1749) π’yi ilk kez bir dairenin çevresinin çapına olan oranını ifade etmek için kullandı. Ancak π’nin bugünkü şöhretini kazanması 1748 yılında matematiğin en büyük isimlerinden biri olan Leonhard Euler’in bir eserinde bir dairenin çevresinin çapına olan oranını belirtmek için π’yi kullanmasıyla gerçekleşmiştir. πdeğerini hesaplamak için kullandığı formüllerin birinde π’nin kendinden sonra gelen kuvvetlerini veren serinin ilkiydi:



Yorumlar2
off aradığım sey burda yok ama osun güzel olmus
biz dairenin tarihçesini istiyoruz siz bize pi,yi veriyorsunuz.
Yorumlarınızı Bekliyoruz
Yorum Yazın
Yorum Yapın