Konigsberg, Almanya’da bir kasabadır. Bu kasaba başka bir nehir ile birleşen Pregel nehrinin etrafında kurulmuştur.İki nehrin birleştiği yerin ortasında bir ada yer almaktadır. Adayı ve nehirlerin iki tarafındaki kasabayı farklı bölgelerini birleştiren yedi tane köprü vardır. 18. yüzyılda Königsberg’in belediye başkanı her gün kasabayı gezmektedir. Ancak her seferinde bir köprüden iki defa geçmektedir. Her köprüden yalnız bir defa geçmek üzere bütün kasabayı dolaşması mümkün olmamaktadır. Bunusorun Euler’in dikkatini çeker.

KÖNİGSBERG KÖPRÜLERİ

Konigsberg, Almanya’da bir kasabadır. Bu kasaba başka bir nehir ile birleşen Pregel nehrinin etrafında kurulmuştur.İki nehrin birleştiği yerin ortasında bir ada yer almaktadır. Adayı ve nehirlerin iki tarafındaki kasabayı farklı bölgelerini birleştiren yedi tane köprü vardır. 18. yüzyılda Königsberg’in belediye başkanı her gün kasabayı gezmektedir. Ancak her seferinde bir köprüden iki defa geçmektedir. Her köprüden yalnız bir defa geçmek üzere bütün kasabayı dolaşması mümkün olmamaktadır. Bunu sorun Euler’in dikkatini çeker.

Königsberg köprüleri Problemi

1736'da İsviçre’li matematikçi ve fizikçi olan Leonhard  Euler  ‘Königsberg köprüleri problemi’ olarak bilinen problemi çözer. Matematiksel olarak yedi köprüden her birini yalnız bir kere geçmek kaydıyla yürümenin mümkün olmadığını ispatlar.

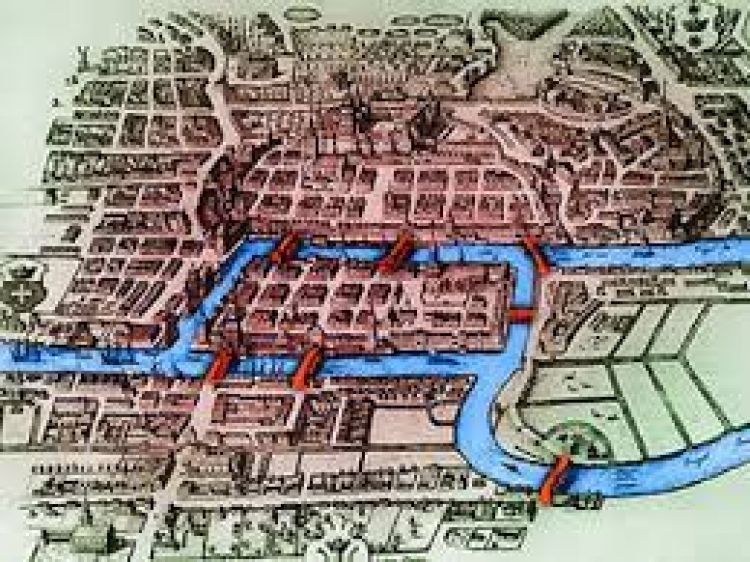
Königsberg köprülerinin bir şeması

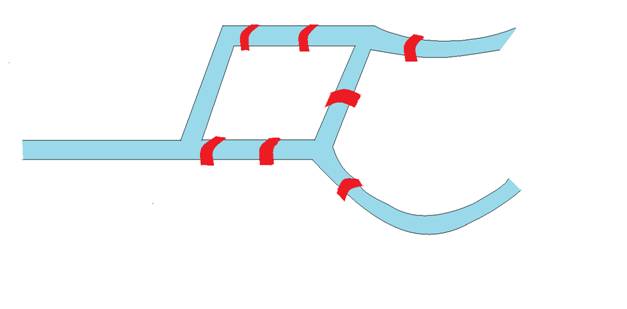
Köprülerden geçmek için yapılan birkaç deneme aşağıda verilmiştir.

• Başarısızlıkla sonuçlanan bir deneme aşağıda görülmektedir.

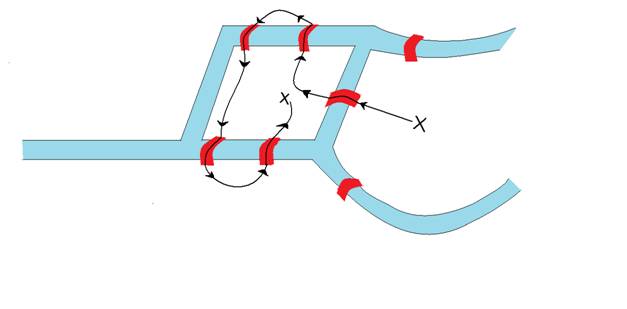
ØBaşarısızlıkla sonuçlanan başka bir deneme aşağıda görülmektedir.

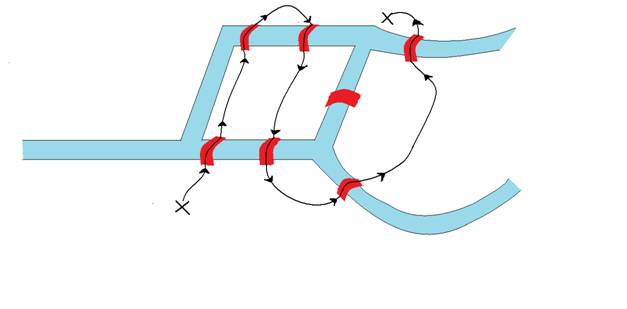
Konigsberg’de aşağıdaki şekilde olduğu gibi bir tane eksik köprü yapılmasına karar verilmiş olduğunu varsayalım:

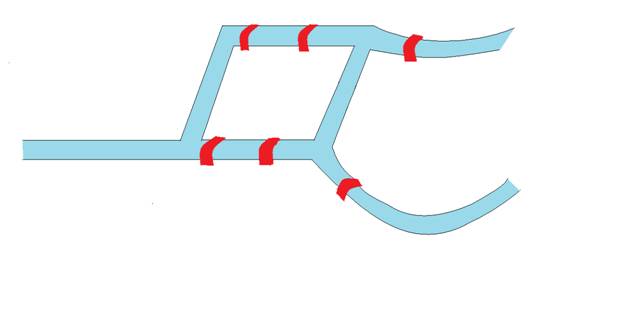
ØBu problem çözülebilirdir. Çözümlerden biri aşağıdaki şekildeki gibidir.

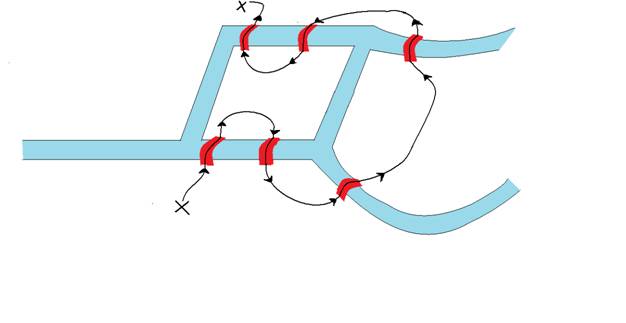
Gerçek Konigsberg probleminden bunun farkı nedir? Her bir kara parçasına giden kaç köprü

vardır?

Bir tek parça kara parçasına tek sayıda köprünün olması neden problem olmaktadır?
Hangi köprüyü eksik almamız durumu farklı yapar mı? Eğer köprü sayısını arttırırsak ne olur?

Bazı grafikler çizip ve her bir durumda bazı yolculuklar planladığımızda Euler’in aşağıdaki

düşüncesine varırız.

Könisberg’deki kara parçalarını noktalarla ve köprüleri eğri parçaları ile gösterirsek aşağıdaki şekli elde ederiz.

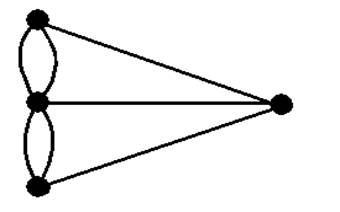
Königsberg köprüleri problemine matematiksel bakış

Tanım: Birbirine bağlı eğriler veya doğrular (edges) ile noktalardan (vertices) oluşan şekle bir grafik denir.

Şimdi problem, bir çizgiden bir daha geçmeksizin ve kalemi kağıttan kaldırmaksızın bu şekli çizme problemine dönüşmüş olur.

Tanım:Eğer bir grafikte bir noktaya tek sayıda eğri bağlı ise bu noktaya tek mertebeden bir nokta , aksi takdirde çift mertebeden nokta denir.

Euler'in Çözümü:

Euler’in Königsberg köprüleri probleminin çözümünde grafiği çizerken işlemin ortasında bir noktaya gelindiğinde bu noktaya bir tane gelen bir tane de bu noktadan giden eğri olmalı böylece noktanın mertebesi çift olmalıdır. Bu bütün noktalar için doğru olmalı fakat biri çizime başladığımız diğeri de çizimi bitirdiğimiz nokta olmak üzere iki nokta dışında her noktanın mertebesi çift olmalıdır ve böylece ilgili grafiğin çizilebilir olması için gerek ve yeter koşul en fazla iki tane tek mertebeden noktasının olmasıdır. ( Başlangıç ve bitiş noktasının aynı olabilir ki bu durumda her noktanın mertebesinin çift olması gerekiyor. ) Şimdi yukarıdaki grafiğe baktığımızda ikiden fazla tek mertebeden nokta olduğunu görüyoruz. Ve böylece grafiğin çizile-

meyeceğini söyleriz. Yani Königsberg ‘deki yürüyüş turu imkansızdır. Burada çizimden kastımız bir çizgi ya da kenardan ( veya eğri parçasından) bir daha geçmeksizin çizimin yapılması anlamındadır. Euler’in düşüncesi çözülebilir olan problemlerde başlangıç noktası tek ve bitiş noktasının tek mertebeden olması gerektiğini vermektedir.

Aşağıdaki grafda her noktanın mertebesi yanında yazılı bulunmaktadır. Aşağıdaki şekilde Königsberg köprüleri probleminde her bir noktanın mertebesini görmekteyiz.

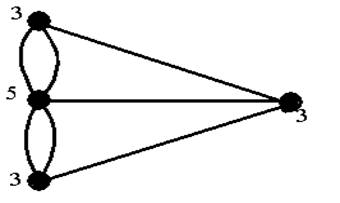
Königsberg’ de aşağıdaki şekilde olduğu gibi bir tane fazla köprü yapıldığını yani sekiz tane köprü kurulduğunu varsayalım. Bu durumda bir köprüden (çizgiden) bir daha geçmeden bütün köprülerden geçilebilir mi? Evet geçilebilir.

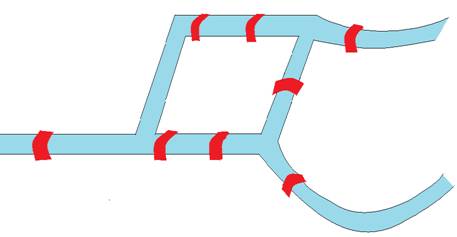
• Sekiz adet köprü yapıldığında aşağıdaki şekil örnek bir çözümü gösterir.

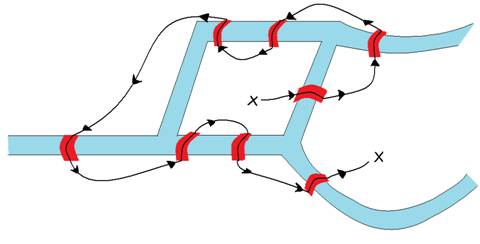
Königsberg köprüleri probleminin Graf Teorisine Genelleştirmesi

Tanım:Birbiriyle kesişmeyen eğriler(arklar) ile birbirine bağlı noktalardan (vertices) oluşan bir şekle bir network denir.

Aşağıdaki networkda her bir noktaya (vertexe) gelen eğri (edge) sayısını görmekteyiz.

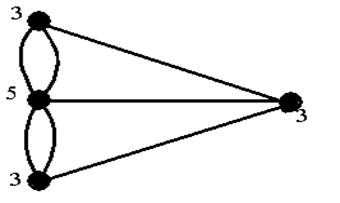
Tanım:Her bir eğri parçasından yalnız bir defa geçen sürekli yola (eğriye) Euler yolu denir.

Teorem:Eğer bir network ikiden fazla tek mertebeden noktaya sahipse Euler yoluna sahip değildir.

Euler bu teoremin karşıtını da ispatlamıştır.

Teorem:Eğer bir network iki ya da ikiden az sayıda tek mertebeden noktaya sahipse bir Euler yoludur.

Problemler:

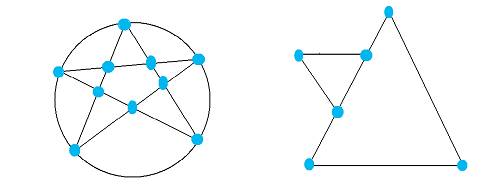
Aşağıdaki her bir grafın Euler yoluna sahip olup olmadığını bulunuz, eğer sahipse bir Euler yolu bulunuz.

                                       Şekil 1                                                                         şekil 2

     Graf (network) bir Euler yoludur. Graf bir Euler yoludur.

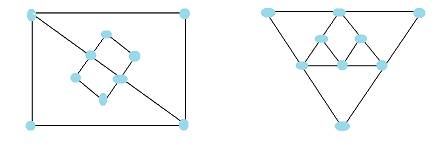
                               şekil 3                                                                  şekil 4

Graf bir Euler yoludur. Graf bir Euler yoludur.

                           şekil 5                                                                                                şekil 6

Graf bir Euler yolu değildir. Graf bir Euler yolu değildir.

Çünkü her ikisinde de dört tane tek mertebeden nokta vardır.

Matematik tarihindeki önemi

Leonhard Euler’in bu araştırmaları matematikte tamamıyla yeni bir dal olan

Çizge kuramının  ilk teoremi  ve topolojinin keşfinin habercisi olmuştur. Çözümün ardından Euler, "Solutio problematis ad geometriam situs pertinentis" isimli makaleyi yayımlamıştır.

Çözümün kullanım alanları

Ayrıt rotalama problemleri, pek çok araştırmacının üzerinde çalıştığı bir rota en iyilemesi problemidir. Bu problemin, gerçek hayatta mektup dağıtımı, yol bakımı, kar temizleme, çöp toplama, devriye araçları ve yol tuzlama konularında pek çok uygulaması vardır. Gerek hükümetler gerekse de işletmeler her yıl bu işlemler için önemli harcamalar yapmaktadırlar. Fakat planlamanın etkin olarak yapılamaması durumunda önemli miktarlarda kaynak israfı söz konusudur.