Doğruda ve Üçgende Açılar Konusu
Geometrik Kavramlar ve Doğruda Açılar
Geometri dersinde başarılı olmak için geometrik kavramlar hakkında bilgi sahibi olmamız gerekir. Aynı zamanda ilerideki konularda sık karşımıza çok çıkacak açı kavramı üzerinde durmalıyız.
Geometrik Kavramlar
Geometri dersine ait terimlere geometrik kavramlar denir. Şimdi en önemli geometrik kavramları tanıyalım.
Nokta: Boyutu yoktur. Kalem ucunun kağıtta bıraktığı izdir. Büyük harfle gösterilir.
Doğru: Her iki yönde sonsuza kadar devam eden noktalar kümesidir.
Düzlem: Nokta ve doğruları içeren 2 boyutlu zemindir.
Işın: Belirli bir noktadan başlayarak sonsuza kadar giden yönlü doğrudur.
Doğru parçası: Başlangıcı ve bitişi olan doğru kesitidir. İki taraftan da sonsuza gitmez. Geometrik şekillerde kullandığımız çizgiler doğru parçalarıdır.
Koordinat sistemi: İki boyutlu uzayı temsil etmek için oluşturulmuş doğru sistemi.
Açı:Kesişen iki doğrunun bir birine göre konumunu bildiren ölçüm birimi.
Üçgen: Üç kenarlı, kapalı, geometrik şekil.
Çokgen: En az üç kenarı olan, kapalı geometrik şekil. Üçgen de bir çokgendir.
Açıortay: Açıyı ortadan ikiye ayıran doğru parçası ya da ışın.
Kenarortay: Kenarı iki eşit parçaya ayıran doğru parçası ya da ışın.
Dar açı: Ölçüsü 90 dereceden küçük olan açı.
Dik açı: Ölçüsü 90 dereceye eşit olan açı.
Geniş açı: Ölçüsü 90 dereceden büyük olan açı.
Doğru açı: Ölçüsü 180 derece olan açıdır.
Tam açı: Ölçüsü 360 derece olan açıdır.
Tümler açı: Toplamları 90 derece olan iki açının birbirine göre durumu.
Bütünler açı: Toplamları 180 derece olan iki açının birbirine göre durumu.
Doğruda Açılar
Geometri dersi içerisinde açılarla çok sık karşılaşırız. Birçok geometrik şeklin içerisinde açıları göreceğiz. Açıların karşımıza çıktığı ilk yer doğrulardır.
Doğruda açı geometrik hesaplamaların yapıldığı ilk konudur. Burada gerekli kavramları bilirsek işlem yapmamız kolaylaşır.
İki doğru kesişiyorsa çapraz açıların ölçüsü birbirene eşit olur. Bu açılara ters açı denir.
Ters açılar, iç ters açılar, dış ters açılar ve yöndeş açılar eşittir.
Doğruda açılar konusu, kesişen ve paralel doğruların birbirine göre durumları ile ilgilidir.
Üçgende Açılar
Üçgende açılar konusunu iyi anlamak için önce üçgeni iyi anlamamız gerekir. Doğrusal olmayan üç noktayı birleştiren doğru parçalarının birleşim kümesine üçgen denir.
Üçgende açılar konusunu iyi anlamamız için bir önceki konu olan doğruda açılar konusunu da iyi bilmemiz gerekir. Zaten üçgendeki açı problemlerinin önemli bir kısmı da bu konudan edindiğimiz bilgi ile çözülmektedir.
Şekildeki ABC üçgeninde [AB], [AC] ve [BC] üçgenin kenarlarıdır. Bu üç doğru parçasının birleşmesiyle bir üçgen ortaya çıkmıştır. Küçük harfle gösterilen a, b, ve c üçgenin iç açılarıdır. Yine aynı şekilde x, y ve z de üçgenin dış açılarıdır. Üçgende iç ve dış açılar, kenarlar temel elemanlardır.
Üçgende Açılar İçin Yardımcı Elemanlar
Üçgende birçok yardımcı elemanlar vardır. Bu yardımcı elemanlar üçgene çeşitli özellikler katarlar. Bu şekilde ortaya çıkan yeni yapılarda açıları hesaplamaya çalışırız.
Üçgende Açıortay
Açıortay kavramını geometrik kavramlar ve doğruda açılar konusunda gördük. Burada da değişen bir şey yok. Açıyı eşit iki parçaya ayıran doğru parçasına açıortay denir. Üçgende olduğu zaman eğer iç açıyı ikiye bölüyorsa iç açıortay, eğer dış açıyı ikiye bölüyorsa dış açıortay şeklinde tanımlanır.
Üçgende Kenarortay
Kenarortay kenarı iki eşit parçaya ayıran ve karşıdaki köşeden çıkan doğru parçasıdır. Üçgende açılar konusunda açıortayla birlikte çok kullanılan elemanlardan biridir.
Kenar Orta Dikme
Bir kenarı ortadan iki eşit parçaya ayıran doğru eğer dikse buna kenarortay dikme denir.
Yükseklik
Bir kenara dik bir şekilde karşı köşeden çıkan doğru parçasına denir. Yükseklik üçgen içinde olabildiği gibi üçgen dışında da olabilir. Üçgende alan hesaplamalarında çokça kullanılır.
Üçgende Açı ve Kenarlara Göre Sınıflandırılma
Üçgenler açı ve kenarlarına göre sınıflandırılabilirler. Açılarına göre üçgenler dar açılı üçgen, dik açılı üçgen ve geniş açılı üçgen şeklinde sınıflandırılır. Kenarlarına göre ise çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgen şeklinde sınıflandırılır.
Dar Açılı Üçgen
Üç açısının hepsi 90 dereceden küçük olan üçgen dar açılı üçgendir. Kağıda düzgün bir şekilde çizdiğimiz üçgen genellikle dar açılı üçgen olur.
Yukarıdaki üçgende α, β ve θ açıları 90 dereceden küçüktür. Bu nedende bu üçgen dar açılı bir üçgendir.
Dik Üçgen
Bir açısı 90 derece olan üçgene denir. 90 derecelik açıyı oluşturan kenarlara dik kenar denir. 90 derecelik açının karşısındaki kenar ise en uzun kenardır ve bu kenara hipotenüs denir.
Geniş Açılı Üçgen
Açılardan birinin ölçüsü 90 dereceden daha büyük olan üçgen şeklidir. Bir açı geniş olduğu için diğer açılar genellikle oldukça dar olmaktadır.
Geniş açılı üçgende yüksekliklerden bazıları üçgen dışarısında olmaktadır.
Çeşitkenar Üçgen
Kenar uzunlukları farkı ölçülerde olan üçgenlere çeşitkenar üçgen denir. Üçgenlerde açılar kenar uzunluklarıyla doğru orantılı olduğu için farklı kenarlar farklı açı ölçüleri demektir. Yani çeşitkenar bir üçgende hem 3 kenar uzunluğu hem de 3 açı ölçüsü farklıdır. Aksi belirtilmediği sürece biz üçgenleri çeşitkenar üçgen olarak varsayarız.
İkizkenar Üçgen
Kenarlarda ikisinin uzunluğu birbirine eşit olan üçgene ikizkenar üçgen denir. İkizkenar üçgende eşit kenarların karşısındaki açılar da doğal olarak birbirine eşit olmaktadır. İkizkenar üçgende eşit kenarların eşitliğini gösteren bir simge genellikle her iki kenar üzerinde de bulunur.
Eşkenar Üçgen
Üç kenarı da eşit uzunlukta olan üçgene eşkenar üçgen denir. Eşkenar üçgende üç kenar da eşit uzunluktadır. Bunun sonucunda üç açısın ölçüsü de eşit olmaktadır. Bir üçgenin iç açıları toplam derecesi 180 olduğuna göre bir eşkenar üçgende her bir açının ölçüsü de 60 derece olacaktır.
Üçgende Açı Özellikleri
Yukarıdaki üçgende açılar için gerekli kavram bilgisi verilmiştir. Üçgende açı sorularının çözülebilmesi için üçgende açı özelliklerinin kavranması gerekir. Üçgende açı özellikleri birbiriyle bağlantılı olan çok sayıda açı kurallarından oluşmuştur. Aşağıda liste halinde en yaygın üçgende açı özellikleri bulunmaktadır.
- Bir üçgenin iç açıları toplamı 180 derecedir.
- Bir üçgenin dış açıları toplamı 360 derecedir.
- Bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir.
- Eşit uzunluktaki kenara bakan açıların ölçüleri eşittir.
- Eşkenar üçgenin bütün açıları 60 derece ve bütün kenar uzunlukları eşittir.
- Bir üçgenin iç açıortayları bir noktada kesişirler.
- Bütünler iki açının açıortayları arasındaki ölçü 90 derecedir.
Yukarıdaki kurallar baz alınarak ve bu kurallardan çıkan sonuçlar kullanılarak bütün üçgende açı problemleri çözülebilir. Şimdi üçgende açı özelliklerinin uygulama alanlarını gösterelim.
Yukarıdaki şekilde gördüğünüz gibi ölçüsü x ve y olan iki iç açıya komşu olmayan dış açının ölçüsü x + y olmaktadır. Aslında bu kural bir üçgenin iç açıları toplamı ile bir doğru açının ölüsünün aynı ve 180 derece olmasından kaynaklanmaktadır. Diğer açının ölçüsüne mesela z dersek hem üçgen açıları toplamı hem de doğru açının ölçüsü x + y + z = 180 olur.
Şimdi gerçek sayılarla bununla ilgili bir örnek çözelim.
Yukarıdaki üçgende ölçüsü x olan DAC açısı verilmiştir. Buna göre x kaç derecedir?
Çözüm: Bir dış açının kendisine komşu olmayan iki iç açının toplamının ölçüsüne eşit olduğunu biliyoruz. Buradan da x = 60 + 35 = 95 derece olur.
İkinci yol: Herhangi bir kurala bağlı kalmadan sadece üçgen iç açıları toplamının 180 olduğunu bilsek de yeterlidir. İki açının ölçüsünün toplamı 95 derece olduğuna göre üçüncü ölçüsü 85 derece olacaktır. Üçüncü açısının dış açısı olan x ise 85 derecenin bütünleridir. Çünkü ikisi birlikte bir doğru açı oluşturmaktadır. Bu nedenle bu açının ölçüsü 180 - 85 = 95 derece olur yine.
Gördüğünüz gibi bir kuralın geliş noktasını bilirseniz bunu ezberinizde tutmak zorunda da kalmazsınız. Üçgende açı problemlerini hep bu mantıkla çözmeliyiz.
Yukarıdaki konkav dörtgen yine bir kuralı ifade etmektedir. Aslında bu kural da aynı mantıklı ortaya çıkmaktadır. C noktasından karşı kenara bir doğru parçası çizdiğinizde ve bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir kuralını uyguladığınız zaman elinize aynı form gelecektir.
Üçgende açılara ait başka bir özelliği kullanıp bir örnek soru daha çözelim.
Yukarıdaki üçgende komşu iç ve dış açıortaylar verilmiş ve x açısının ölçüsü sorulmaktadır.
Çözüm: Dikkat ederseniz ortadan açıortayla ikiye ayrılmış iki açının bütünler açılar olduğunu fark edersiniz. Bütünler açıların toplam ölçüsü 180 derecedir. Yani bu soruda nokta ve çizgiyle gösterilen açılardan 2 nokta açısı + 2 çizgi açısı = 180 derecedir. Bu durumda 1 nokta + 1 çizgi açısı = 90 olur. Yani (NAD) açısının ölçüsü 90 derecedir. Bu durumda 90 + 28 = 118 derece yapmaktadır. Dikkat ederseniz bu iki açıya x açısını da eklediğimizde bir üçgen ortaya çıkmaktadır. Bu durumda x =180 - 118 = 62 derece olur.
Bu örnek soruda da aslında mantığımızı kullanarak yukarıda bahsettiğimiz başka bir kuralı ortaya çıkardık. Bütünler iki açının açıortaylarının toplamının 90 derece olduğunu yukarıda zaten söylemiştik.
Üçgende Açılar Soru Çözüm Yöntemleri
Üçgende açılar sorularını çözerken takip edilmesi gereken bazı önemli yöntemler vardır. Bu yöntemleri takip etmek üçgende açılar konusuna ait soru çözümünü en iyi şekilde yapmayı sağlar. Öncelikle bütün geometri konularında olduğu gibi işleme başlamadan önce soru kısmını detaylı bir şekilde okumalısınız. Çünkü üçgen şeklin üstünde belirtilmemiş bazı bilgiler soruda verilmiş olabilmektedir.
Geometri sorularında işlem yapmaktan kaçınmamak gerekir. Bu işlem yapma boş açı ve uzunluklara harfler vererek denklem eşitlikleri elde etme şeklinde olmaktadır. Ayrıca üçgende açı sorularında gerekli gördüğünüz yerde çizgiler çizerek yeni üçgenler elde etmekten kaçınmamalısınız. Bu şekilde soruyu daha kolay bir forma getirebilirsiniz.
Aşağıda 2009 yılında üniversite sınavının ikinci bölümünde çıkmış bir üçgende açılar sorusu bulunmaktadır.
Gördüğünüz gibi soru gayet standart bir üçgende açılar sorusudur. Her zamanki gibi belirli bilgiler verilmiş ve x açısının ölçüsü sizden istenmektedir. Bu sorunun çözümünü açılara harfler vererek gerçekleştirelim.
Çözüm: DAC üçgeni için 65 derecelik açı bir dış açıdır. Dolayısıyla kendisine komşu olmayan a ve b açılarının toplamına eşittir.
Bu durumda a + b = 65 olur. Şimdi en büyük üçgene baktığımız zaman ise x + a + a + b + b = 180 eşitliğini rahatlıkla kurabiliriz. Bu durumda x + 2(a+b) = 180 olacaktır. Yukarıda elde ettiğimiz eşitliği kullanırsak da x + 2.65 = 180 ⇒ x + 130 = 180 ⇒ x = 50 derece eşitliğini elde ederiz.
Bu örnek soruda görüldüğü gibi bilmediğimiz açılara harf verip eşitlik kurmak üçgende açılar soruları için çok önemlidir. Elde edilecek olan eşitlikler birinci dereceden basit denklemler olacaktır.
Doğruda ve Üçgende Açılar ile İlgili Yazılar
Üçgende Açı-Muhteşem Üçlü Sorusu
Üçgende açı konusunda dikkatimi çeken iyi bir açı bulma sorusu.Genelde bu tip sorularda muhteşem üçlü oluşturulmaya çalışılır.Umarım bu soruyu benim kadar sizde beğenirsiniz.Cevabı en kısa zamanda yorum olarak makalemizin altına eklenecektir.
Üçgende Açı Çıkmış Çözümlü Sorular
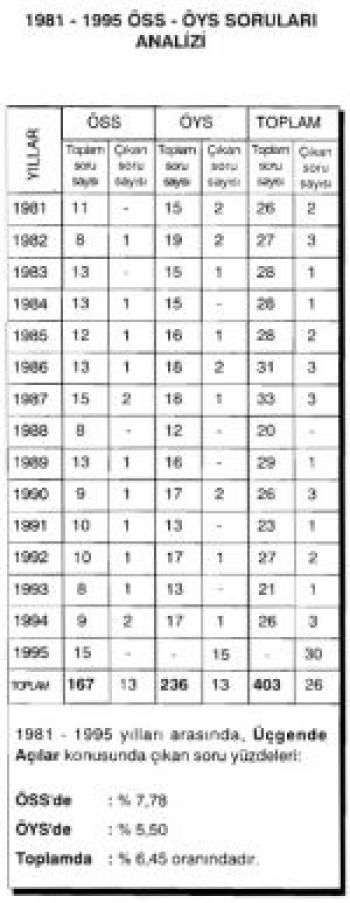
Üçgende açılar konusundan öss ve öys de çıkmış çözümlü sorulara bu makalemizde bulabilirsiniz.Üçgen de açılar konusuyla ilgili sormak istediğiniz tüm soruları aşağıdaki yorum bölümüzden sorabilirsiniz.Aşağıdaki oranlarda da göründüğü gibi sınavda üçgen de açı konusundan yaklaşık %6 oranında çıkmaktadır.Bu orandan da görüldüğü gibi ygs de çıkan 10 geometri sorusundan 1 tanesinin üçgende açı konusundan olma ihtimali yüksek.