Trigonometri Konusu
Trigonometri Konu Anlatımı
Matematikte öğrencilerin en çok zorlandığı konuların başında trigonometri gelir. Bu ders notunda trigonometriyi basitleştirerek anlatacağız. Konuyu biraz öğrendikçe zor olmadığını, aksize zevkli olduğunu fark edeceksiniz. Trigonometriyi öğrenmek özellikle türev ve integral konularında çok işimize yarayacaktır. Bu nedenle konuyu dikkatlice detaylı çalışmanızı tavsiye ediyoruz.
Bir açıyı çizmek için iki kenara ihtiyacımız vardır. Açıyı daraltıp genişlettikçe bu iki kenarın birbirine göre durumları da değişecektir. Bu nedenle her açının kendine ait bir uzunluk oranı vardır. Bu oranı en iyi dik üçgende görebiliriz.
Matematiğin açı ve kenar arasındaki ilişkileri inceleyen dalına trigonometri deriz.
Temel Trigonometrik İfadeler
En temel dört tane trigonometrik ifade vardır:
- Sinüs (sin)
- Kosinüs (cos)
- Tanjant (tan)
- Kotanjant (cot)
Bunları dik üçgen üzerinde gösterelim. Böylece temel trigonometrik ifadelerin dik üçgen üzerinden nasıl ortaya çıktığını anlarız.
Yukarıdaki üçgende verilen eşitliklerin çok iyi anlaşılması gerekir. Bu eşitlikler anlaşılırsa konunun geri kalanı daha iyi anlaşılacaktır.
Öyleyse yukarıda denklemlerden tanα = sinα / cosα ve cotα = cosα / sinα bulunacaktır. Bunları kendiniz de deneyip ispatlayabilirsiniz. Hatta bunu yapmanız çok da iyi olacaktır. Buradan tanα = 1/cotα ve cotα = 1/tanα bulunacaktır. Yani tanjant ve kotanjant birbirinin tersi fonksiyonlardır. Dolayısıyla tanα.cotα = 1 olacaktır.
Tanjant ve kotanjant arasındaki ilişkiyi iyi bilmek çok önemlidir.
Soru: tan32°.cot32° = ? Çözüm: Açı aynı olduğu zaman tan.cot çarpımı 1 e eşit olur.
Tümler İki Açı Arasındaki Trogonometrik Eşitlikler
Toplamları 90° olan açılara tümler açılar denir. Örneğin 50° ile 40° tümler iki açıdır. Temel trigonometrik ifadeleri dik üçgen üzerinden tanımlamıştık. Öyleyse bir açının sinüsü diğer açının kosinüsü olacaktır. Buradan da şu eşitlikler çıkacaktır:
- Sekant (sec) = 1/cos
- Kosekant (cosec) = 1/sin
Tümler açılarla ilgili eşitlikleri trigonometrinin her seviyesinde kullanmaktayız. Bu nedenle bu konuyla ilgili bol miktarda soru çözmek gerekir.
Soru: sin42° / cos48° + cos48° / sin42° işleminin sonucu kaçtır?
Çözüm: 42 ve 48 tümler açılardır. yani toplamları 90 etmektedir. Öyleyse bu açılardan birinin sinüsü diğerinin kosinüsüne eşittir. Bu nedenle cevap 1 + 1 = 2 olacaktır.
Trigonometri ile İlgili Yazılar
Trigonometri ve Trigonometri Formülleri
Eski Yunanca "üçgen" ve "ölçü" sözcüklerinden meydana gelir.
Trigonometri üçgenlerin kenar ve açılarının hesap yolu ile çözümünü konu eder
Bulunan sonuçlar çok kenarlı şekiller içinde hesaplama sağlar. Bunun için trigonometrik fonksiyonlarda yararlanır
Trigonometri aslında bütün işlemleri birim çember üzerinde yapılan matematiğin bir alt dalıdır. Eğer biraz araştırırsan göreceksin, trügonometrinin o kadar çok alt başlığı vardır ki, belirli bir tanımı zordur. Açı ölçmeye yarar, açıdan alan ile ilgili işlemler yapmaya yarar, açı bölmeye yarar, bir açının trigonometrik değerlerinin bulunmasını sağlar, herhangi iki kenarı ve bir açısı bilinen üçgenin alını ile ilgili işlemler yapmaya yarar..
Trigonometride çıkmış öss sorularını sayfanın devamına tıklayarak indirebilirsiniz
1987-2007 yılları arasında ÖYS-ÖSS sınavında çıkmış çözümlü sorular makelemizin en altındadır..
Trigonometri Cetveli
Trigonometri Cetveli
Trigonometrinin Tarihçesi
TANIM:Matematiğin dogrudan dogruya astronomiden cıkmış bir koludur; bir üçgen kenarlarının veya açılarının ölcülerini bunlar içinden bazılarına dayanarak hesaplamaya olanak sağlar.
TARİHÇE: Babilliler ve Mısırlılar;gökbilim gözlemlerine ve piramitlerin yapımına ilişkin ttrigonometri elemanlarına sahiptiler. Yunanlılar Menelaus'un küresel geometrisine dayanarak gemicilikte gece saatinin belirlenmesi gibi pratikte kullanılmak üzere nicel bir gökbilim hazırladılar.İskenderiyeli Hiparkhos ve Ptolemaios bir çember yayıyla bunu gören kirişlerin uzunlukları arasindaki bagıntılarısistemli bir biçimde incelediler. Çemberin daha yeni olan 360 dereceye bölünmesine dayalı olarak , bu bölümlere karşılık gelen kirişler, merkez açının yarısının sinüsüne eşdeğerdir. Çağdaş dilde sinA ve sinB ye dayanarak sin(a-b) yi hesaplamaya olanak veren Ptolemaios teoremi, (3/4) derecelik bir aralık için, onu trigonometrik cetveli düzenlemeye yöneltti; bu aralık ötesinde yaklaştırılma işlem yapılır.Hint trigonometrisi yarım yaya, bunu gören yarı kirişi eşlik ettirerek bu günki sinüs kavramına dahaçok yaklaşıyor.
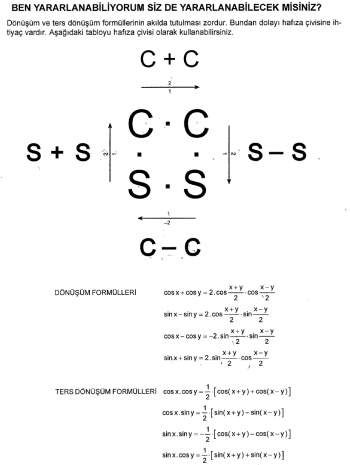
Trigonometrik Dönüşüm ve Ters Dönüşüm Formülleri Nasıl Ezberlenir?
Dönüşüm ve ters dönüşüm formüllerinin akılda tutulması zordur. Bundan dolayı hafıza çivisine ihtiyaç vardır.Trigonometri dönüşüm ve ters dönüşüm formüllerini kolay yoldan ezberleminiz için makalemizdeki tablodan yararlanabilirsiniz.
Trigonometrik Formüller Videolu Anlatım
Trigonometrik Dönüşüm ve Ters Dönüşüm Formülleri Nasıl Ezberlenir.Mükemmel Yöntem (kitaplarda yok sadece bizde)
Videolu Anlatım