Diziler ve Seriler Konusu
Diziler
ARİTMETİK DİZİ
TANIM
d sayısına da aritmetik dizinin ortak farkı denir.
GENEL TERİM
İlk terimi ve ortak farkı d olan (
) aritmetik dizisinin genel terimini
ve d türünden bulalım:
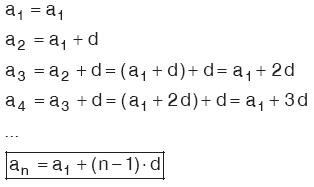
ARİTMETİK DİZİNİN ÖZELLİKLERİ
p < n olmak üzere, bir aritmetik dizinin; genel terimi,
ortak farkı,
Sonlu bir aritmetik dizide, baştan ve sondan eşit uzaklıkta bulunan terimlerin toplamı birbirine eşittir.
x ile y gibi iki reel sayı arasına n tane terim yerleştirilerek oluşturulan (n + 2) terimli aritmetik dizinin ortak farkı,
şeklindedir.
Bir aritmetik dizide, her terim kendisinden eşit uzaklıktaki iki terimin aritmetik ortalamasına eşittir.
Bir aritmetik dizinin ilk n teriminin toplamı olsun. Buna göre,
Bir aritmetik dizinin ilk n teriminin toplamı olsun. Buna göre,
GEOMETRİK DİZİ
TANIM
Ardışık her iki terimi arasındaki oran eşit olan diziye geometrik dizi denir.
Yani her n pozitif tam sayısı için,
olacak şekilde bir varsa, (
) dizisine geometrik dizi;
r sayısına da geometrik dizinin ortak çarpanı ya da ortak oranı denir.
GENEL TERİM
İlk terimi ve ortak oranı r olan (
) geometrik dizisinin genel terimini
ve r türünden bulalım:
GEOMETRİK DİZİNİN ÖZELLİKLERİ
p < n olmak üzere, bir geometrik dizinin; genel terimi,
ortak farkı,
x ile y gibi iki reel sayı arasına n tane terim yerleştirilerek oluşturulan (n + 2) terimli geometrik dizinin ortak çarpanı,
şeklindedir.
Sonlu bir geometrik dizide, baştan ve sondan eşit uzaklıkta bulunan terimlerin çarpımı birbirine eşittir.
Bir geometrik dizide ilk n terim çarpımı,
Bir geometrik dizide, her terim kendisinden eşit uzaklıktaki iki terimin geometrik ortalamasına eşittir. Diğer bir deyişle, bir geometrik dizide, herhangi bir terimin karesi kendisinden eşit uzaklıktaki iki terimin çarpımına eşittir.
Bir geometrik dizinin ilk n teriminin toplamı olsun.
x, y, z sayıları hem aritmetik hem de geometrik dizi oluşturuyorsa, x = y = z dir.
Hem aritmetik hem de geometrik olan dizi, sabit dizidir.
Sabit dizi, ortak farkı 0 olan aritmetik bir dizi ve ortak çarpanı 1 olan geometrik bir dizidir.
Diziler ve Seriler ile İlgili Yazılar
ARİTMETİK ve GEOMETRİK DİZİLER, SERİLER
Ardışık iki terimin arasındaki fark, aynı sabit bir sayı olan dizilere aritmetik dizi denir. Diğer bir ifadeyle Ɐ ∈N+ için , an+1 – an = d olacak şekilde bir d ∈R varsa (an) dizisine aritmetik dizi, d sayısına da ortak fark denir.
ÖRNEK
(an) = (n+10)/5 dizisinin aritmetik dizi olduğunu gösteriniz. Ortak farkını bulunuz.
an+1 – an = (n+1+10)/5 – (n+10)/5 = 1/5 olduğuna göre (an), ortak farkı d = 1/5 olan bir aritmetik dizidir.
Dizi ve Seriler(Aritmetik Dizi- Geometrik Dizi ve Seri)
DİZİLER Bu bölümde reel değişkenli fonksiyonların limitlerinin hesabında yararlanacağımız reel sayı dizilerini inceleyeceğiz.
DİZİ N+ = {1,2,3,...} olmak üzere f: N+ R şeklinde tanımlanan her fonksiyona reel sayı dizisi denir.
f fonksiyonunun tanım kümesi N+ olduğuna göre, değer kümesinin elemanları f(1), f(2), f(3), ..., f(n), ... dir. Değer kümesinin elemanları
f(1) = a1, f(2) =a2, f(3) =a3, ..., f(n) =an, ... şeklinde gösterilir.
Dizinin 1. terimi, 2. terimi, 3. terimi, ..., n. terimi, ... adı verilir. Dizinin 1. terimine ilk terim, n. terimine de genel terim denir.
a1, a2, a3, ..., an, ... terimlerinden oluşan dizi (a1, a2, a3, ..., an, ...) şeklinde gösterilir.
Bu dizi kısaca (an) şeklinde gösterilir. Buna göre,
(an) = (a1, a2, a3, ..., an, ...) dir. Bir dizi genel terimi ile belirlidir.

